Guess what? The contents of this essay are my opinion. Want to comment, positively or negatively about this? Send me an email: cdoswell@earthlink.net
This essay is a sort of continuation of some ideas I've been ranting about for many years. You can download a PDF file version of an informal publication that discusses certain aspects of the problem, as I see it, here. However, in this essay, I'm going to call attention to what is likely a very well-intended Web site created by the Storm Prediction Center (SPC) - their so-called "Mesoscale Analysis" site - that I believe has some perhaps unintended consequences. It is those unintended consequences that bother me.
I want to emphasize from the start that I'm in no way criticizing the SPC for its efforts to be informative and in fact I applaud their generosity in making available some sampling of the diagnostic tools that are at their disposal. The people who built this site deserve a great deal of credit for their efforts. There is nothing fundamentally wrong with making this content available.
Nevertheless, the SPC is the nation's acknowledged core of expertise in severe storms forecasting. For them to issue a product is to endorse its contents and encourage the use of any products contained on the page. This is not necessarily their intention - I cannot address the issue of their intentions, save to take them at face value - consider their statement of goals for the site:
" This information is provided by SPC as a way of sharing the latest severe weather forecast techniques with local forecasters."
The various items presented on the site are definitely not "forecast techniques" - they're a set of diagnostic variables and composite indices. Beyond that, their forecast value generally has not been established - the fact that many of them have been in continuous use for decades is not remotely sufficient, as I see it, to establish their forecast value. For example, one of the most common and well-established among these is Convective Available Potential Energy (CAPE) in various forms. A few years ago, two colleagues and I (Monteverdi et al. 2003 - available from here) showed that for at least one type of severe weather forecasting - tornadoes in California - CAPE was essentially of no value in discriminating tornado cases from nontornadic cases when used as a forecast variable and the forecasts verified against observations, whereas another variable (0-1 km shear) did have some value in making such discriminations. I note that the SPC Mesoscale Analysis page includes the 0-1 km "shear".
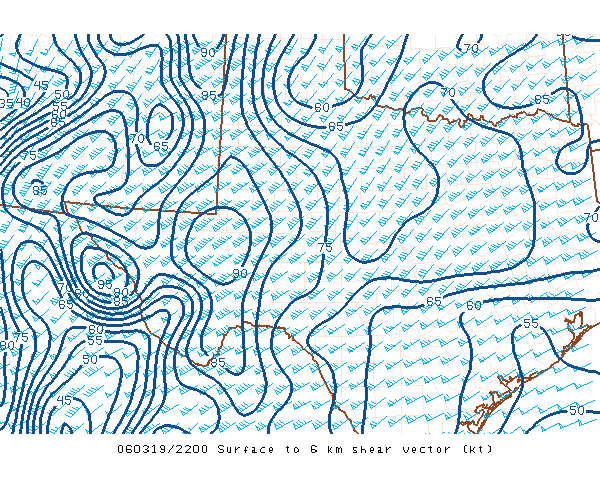
Note: The SPC site expresses "shear" in terms of wind speeds (see figure below), which is dimensionally incorrect. Vertical wind shear is defined as the derivative of the vector wind with height, which has dimensions of (unit time)-1. A wind difference of 10 m s-1 over a depth of 1 km gives a proper shear value of 10-2 s-1. By giving only the magnitude of the vector difference between the wind at the top and bottom of the layer, this is not a proper shear, but only the magnitude of the wind difference vector. For simple layers, such as 0-1 km, the conversion of the SPC "shear " values is easy, but if the layer is not bounded by simple integer values, this "shear" is misleading, since it may not be simple to account for the depth of the layer when computing a proper value.
Generally speaking, it can be said of all of the variables displayed on the SPC site that any one of them considered in isolation, has little forecast value. Any competent severe weather forecaster understands that no single variable could ever be considered even remotely adequate to forecast severe storms, but that isn't the issue here, as I see it. My concern is that virtually all of these variables are diagnostic variables or indices of various sorts. Their values as forecast variables is quite limited for reasons I'm about to explain. They are not generally prognostic variables, plain and simple. They tell you something about the current state of the atmosphere at the time of their calculation, but their capability to inform you about future states of the atmosphere is quite limited, at best.
In what follows, I'll be using the contents of the SPC Mesoscale Analysis page to illustrate the issues that concern me. Again, to reiterate, I'm not being negative about the SPC or those who constructed the site.
Just what do I mean by a "diagnostic variable"? This brings up the topic of diagnosis, a topic I could easily go on about at some length, but will not do se here. An informal publication about diagnosis can be found here. A diagnostic variable is some quantity that either is a basic observed variable (pressure, temperature, wind, humidity, etc.), or can be calculated from those observations. It also can be obtained from the gridded fields produced by numerical weather prediction (NWP) models, such as the so-called RUC, which is the source of model data for the SPC page. The SPC Mesoscale Analysis page uses a combination of observations and model forecasts of observed variables to compute displayed products. To the extent that the RUC model forecasts depart from what would be observed in the real atmosphere, this choice to use a combination of observed and model forecasts data is potentially misleading. But that also is not my main concern in this essay.
Using diagnostic variables, it is possible to establish a quantitative understanding of the current state of the atmosphere. I can look at the winds and visually determine zones of strong rotation (vorticity) and convergence, but without a quantitative evaluation of the vorticity and convergence values, my sense of the strength of those variables is subjective. In meteorology, a quantitative assessment is typically preferred over subjective assessment. There are many good reasons for this, none of which I'm willing to dispute.
Nevertheless, one should be careful in interpreting some diagnostic variables too literally. Consider the divergence / convergence field, expressed in conventional meteorological notation as:.
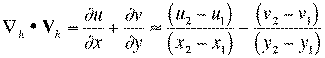
where the subscript h denotes the horizontal
gradient operator and the horizontal vector wind 
- when the wind is expressed in the typical Cartesian coordinate component form.
It's widely recognized in meteorology that divergence calculations tend to be a bit tricky. For one thing, divergence typically is a small difference between two relatively large numbers, which can make the calculation somewhat unreliable. Further, it turns out that the divergence calculation is very much resolution-dependent. Consider:
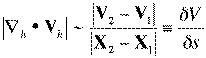
where X denotes a position vector 
. This statement says that the
magnitude of the divergence scales simply as the magnitude of the
wind difference between two points divided by the distance between
them - call it a simple scaling law for the divergence
magnitude. If may not be widely recognized, but the order of
magnitude of the difference in the wind between two points is
not very scale dependent - it typically is of order 1-10 m
s-1. Only rarely does its order of magnitude reach 100 m
s-1, and only rarely is its order of magnitude as small as
0.1 m s-1. Thus, the divergence tends to depend most
strongly on the distance between sample points. If we
calculate divergence from a sparse network of points, such as
rawinsonde sites (~400 km apart), this gives a rough order of
magnitude for the divergence, according to the above scaling rule, of
about (1-10) m s-1 / 400 km = 2.5 x (10-6 -
10-5) s-1. On the other hand, if we use the
network of surface observations (~100 km apart), the foregoing
scaling rule gives a value of 1 x (10-5 - 10-4)
s-1, which is four times larger. As we move toward smaller
scales, the divergence magnitude generally increases, and vice-versa.
Another aspect of the calculation of divergence / convergence is that the calculations can be volatile - that is, relatively small changes in the observed wind vectors (which aren't necessarily known to high accuracy or precision, for a variety of reasons) can produce relatively large changes in the calculations. The fields tend to jump around and behave somewhat erratically, although the basic shape of the fields might be fairly consistent from one time to the next. The consistency of the basic shape of the fields, combined with the volatility of the details is a direct indication of the sensitivity of the details in the field to small changes in the wind. This will be illustrated shortly with diagnostic variable based on the divergence.
The point of this apparently diversionary discussion is to illustrate the point that when using diagnostic calculations, it's quite possible to be misled if you aren't aware of the caveats associated with any diagnostic variable. What are the unique sensitivities in those calculations? How much confidence can you put in the numbers and how they might change over time? Each diagnostic variable has its own story, and if you're to use them properly, you need to be aware of each such story.
There are several classes of diagnostic variables:
The observed variables are the simplest variables to observe with the typical meteorological instruments. Other variables are less simple to observe but may have some valuable property, such as being conserved under certain reasonable assumptions. For example, at the surface, the temperature and dewpoint are the common observed variables. However, for reasons discussed in Sanders and Doswell (1995 - available in PDF form, here), it may be preferable to analyze mixing ratio and potential temperature (illustrated below and available here), which take into account the pressure at the elevation of the surface sites - both are conserved variables for dry adiabatic processes.
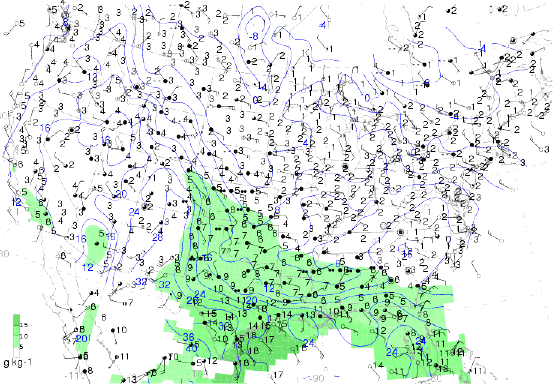
An analysis of surface potential temperature (deg C) - blue contours - and mixing ratio (g kg-1) - green shading with a key to values in the lower left, as provided by the State University of New York at Albany - Atmospheric Sciences
There are many ways to combine the observed variables into deduced variables that are more useful than the raw observations for some specific purpose.
As a primary example of a combined variable, consider the so-called "surface moisture flux convergence (or divergence)" - this has been discussed in some detail by Banacos and Schultz (2005) - available in PDF form here. The formulation of this diagnostic variable can vary from one application to another, but it is often formulated as the finite difference calculation of the quantity:
where r is the mixing ratio - this calculation is typically done using the relatively dense surface observations. This variable is intended to show where surface convergence (i.e., where divergence is negative) is occurring in the presence of moisture. Presumably, the idea is to suggest where upward motion (which generally means that convergence is happening at the surface) is happening in the presence of moisture. The Banacos and Schultz discussion of this term considers several issues associated with this combined variable and I'll not repeat those comments here. I want to emphasize two points about this:
1. Its putative value as a forecast variable has never been firmly established by a carefully-done statistical verification study. Its popularity is based almost entirely on anecdotal evidence and heuristic arguments.
2. It is well-known that the first term on the rhs of the MFC - that associated with surface divergence - is much larger than the second term - that associated with moisture advection. The two components of the major term in this combination - the mixing ratio and the divergence field - can evolve quasi-independently. What this variable shows is where those two main components have come together at the time of the analysis. Thus, this is first and foremost a diagnostic variable.
Because the MFC calculation is dominated by the first term on the rhs, it's volatile in its detail, as is the divergence itself. As suggested when comparing the first field with the second, one hour later,
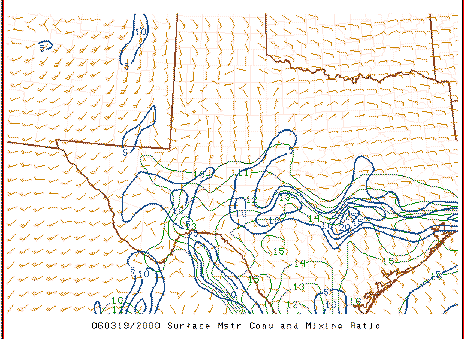
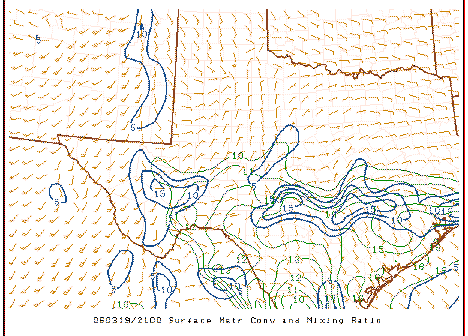
it can be seen that the overall field is fairly similar but where the maxima and minima occur (and the magnitudes of those peaks and valleys) shift about somewhat erratically . Compare the above to the plots of the associated surface observations:
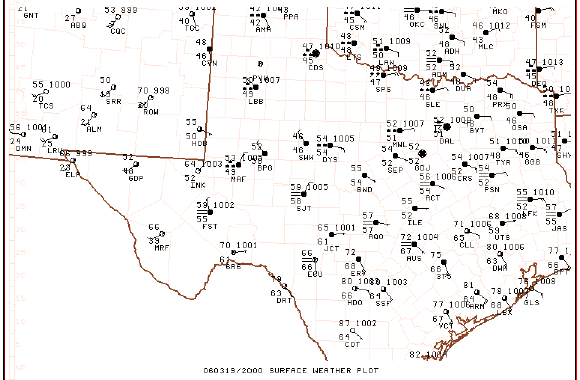
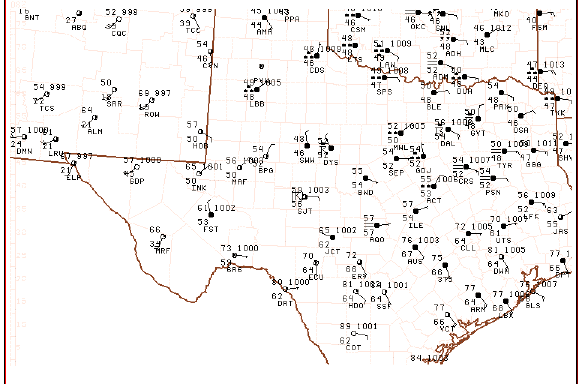
It's apparent from this that the basic structure in this field can be deduced subjectively from the raw observations and that only minor changes in the wind fields are producing the fluctuations in the local strength and magnitude of the surface MFC.
Another example of a combined variable is CAPE. Its calculation is rather involved, but if we reduce that calculation to its most basic elements, large CAPE is generally found where low-level moisture is found in the presence of conditionally unstable lapse rates in the lower mid-troposphere. Again, low-level moisture and lapse rates in the lower mid-troposphere can evolve quasi-independently, and then can be superimposed by differential advection processes. Prior to that superposition, the air streams carrying conditionally unstable lapse rates and low-level moisture (typically at different levels in the atmosphere and so can advect variables in different directions and at different speeds) have not yet interacted and so little or no CAPE is found. The presence of CAPE indicates when moisture and conditionally unstable lapse rates have been superimposed, but an absence of CAPE prior to that superpositioning cannot be used to infer that in the future, large CAPE will not be present. This is, to me, an essential concept for understanding the difference between a diagnostic and a prognostic variable. CAPE informs me where moisture and conditional instability are already superimposed, not where they will (or will not) be superimposed in the future.
Like MFC, CAPE is a relatively volatile parameter.
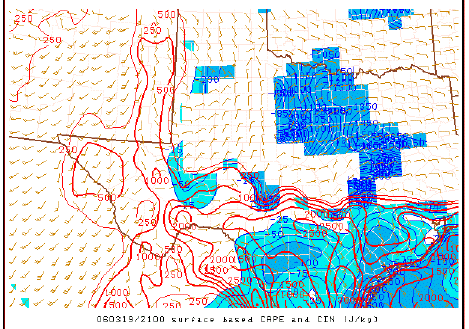
Surface based CAPE, depicted by the red contours, and also the convective inhibition (CIN), depicted by the blue contours - another diagnostic parameter.
By combining variables, in effect, the prognostic value of a combined variable is quite limited, whereas if one were separately monitoring the time and space evolution of the individual combined variables, it may be quite apparent that at some point in the future, they are (or are not) likely to overlap and thus produce large values for the combined variable. Should you choose to use a combined variable in a purely diagnostic sense, to inform yourself about the quantitative implications of your diagnosis, that's a very different and - in my view - much more acceptable way to derive value from such a variable. Using such a variable as a forecast of weather to come is much riskier venture.
Philosophically, the notion of an index has a long history of use in severe storms forecasting, perhaps beginning with the so-called Showalter Index, and continuing on through a growing plethora of constructs, including the Lifted Index (LI), the Sweat Index, the Bulk Richardson Number, the Energy-Helicity Index (EHI), the Supercell Composite Parameter (SCP), and the Significant Tornado Parameter (STP) - to name only a few. These variables tend to be volatile, somewhat like the divergence (and variables defined using the divergence), albeit for different reasons.
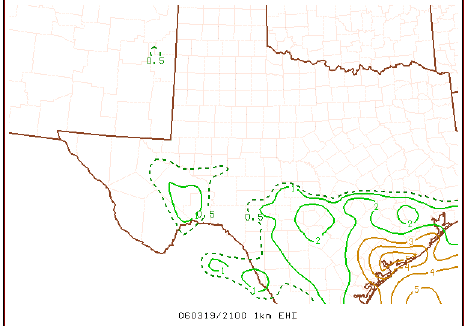
An example of EHI based on the 0-1 km layer
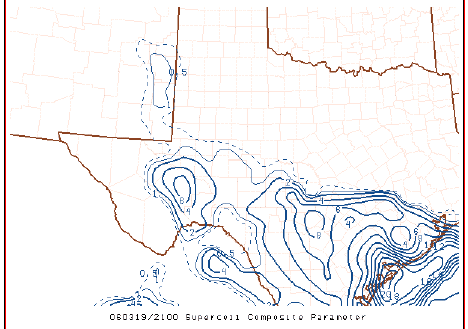
An example of the SCP
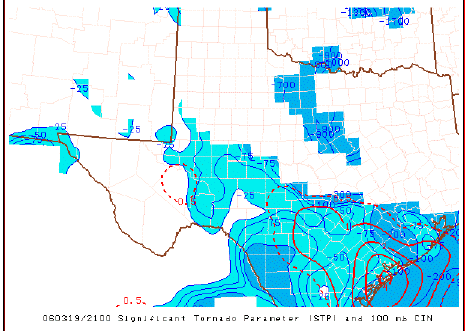
An example of the STP
Such variables are often only vaguely related to any physical argument. The early static indices (e.g. the Showalter and Lifted Indices) are at least based on simple parcel theory, although that and a number of other problems outlined in the essay of mine referenced above make their use as forecast variables problematic. The Bulk Richardson Number is at least related dimensionally (i.e., it's dimensionless) to the true Richardson Number - but the relevance of any Richardson number to the physics of deep moist convection is pretty tenuous. Its original intent was to address topics in turbulence theory.
Many of these indices, including the Sweat Index, the EHI, SCP, and STP, have combined variables in ways that have no physically-based rationale - that is, forming sums, products, and ratios that may include scaling constants that are essentially empirical rather than physical. Those scaling constants are more for convenience than anything else, often being derived from typical values for the input variables in certain situations. The issue is whether or not the variable can be related to something based on physical principles. A diagnostic variable based on physical principles might be something like the static stability tendency, or the potential vorticity, or the energy dissipation rate. Just throwing together two or more variables in some way leaves open too many questions and makes it difficult to relate the variable to any physical understanding of the process.
I've mentioned in the preceding that many potential variables have never been tested as forecast variables. So just what do I think it requires? As already discussed, a diagnostic variable definitely has value in telling you something about the existing state of the atmosphere at the time of the diagnosis, but it might also have predictive capability.
I would say that any proper assessment of a variable as a forecasting tool has to do something along the lines of what we showed in Monteverdi et al. (2003) - develop a classic 2 x 2 contingency table for a "developmental" data set that would look like:
forecast yes event |
forecast no event |
sum |
|
observed yes event |
x |
y |
x+y |
observed no event |
z |
w |
z+w |
sum |
x+z |
y+w |
x+y+z+w=N |
The standard 2 x 2 forecast verification contingency table
This is the standard verification table when considering a dichotomous (yes/no) forecast for some event. To create this for a potential variable, you'd need to pick a threshold value for the possible forecast parameter - forecast "yes" if the variable is at or above the threshold, and "no" if the variable is below the threshold. Using the table above, an assessment of the accuracy of the forecasts using the developmental data set would be done. It's possible to optimize the choice for the threshold value of the variable using the so-called Relative (or Receiver) Operating Characteristic curves associated with signal detection theory - see here for a discussion of this - I won't go into details in this essay - consider it an assignment.
Now, assume you've chosen a threshold for your possible forecast variable and determined the accuracy of the forecasts made using that threshold. In order to do a complete assessment, however, another data set is needed that's completely independent of the developmental data set - for purposes of this paper, a wholly different set of cases than those used for development and testing of the threshold values for the variable (including assessing the forecast accuracy for the developmental data set). If the results using the independent data are comparable to those found from the developmental data, confidence in the use of the variable as a forecast variable is correspondingly high. If there's a big difference between the results from the two data sets, then perhaps a bigger sample is needed, but in any case, confidence in the forecast value of the variable (and its associated threshold value) is correspondingly low.
In the case of the diagnostic variables discussed in this essay, their potential as a forecast variable requires them to exhibit a reasonable level of forecast accuracy when applied in this way- that is, as diagnosed at some time before the event. It's plausible to believe that some or most of the variables shown on the SPC site could have some forecast potential, but it would have to be shown just how accurate they can be by filling out the whole contingency table (including the "w" box - correct forecasts of non-events!) and considering some measures of forecast accuracy. Verification of forecasts is quite a science in its own right and deserves some careful consideration.
Furthermore, I'd guess that the accuracy of any diagnostic variable used as a forecast variable would increase as the time between the diagnosis and the event decreases. Thus, you would need to develop contingency tables and full assessments as described above for a variety of diagnosis times relative to the beginning of the forecast events - say, 12 h, 6 h, 3 h, and 1h before the actual events begin. The accuracy of the variable as a forecast variable would then be known as a function of time before the event - surely that would be a necessary component of a complete assessment.
Of course, this is not the only way to assess the accuracy of a forecast variable, but it does represent a sort of standard I believe is necessary before asserting that a diagnostic variable has real value to forecasters. That is, anything not comparably rigorous is simply not sufficient. Is this a tough standard? Yes. Can someone get by with less? Depends on what you mean by "get by" I suppose - but I believe that anything less rigorous is not going to be very convincing, at least for me.
In my experience, many forecasters, implicitly or not, are seeking a "magic bullet" when they offer up yet another combined variable or index for consideration. If forecasting were so simple as to be capable of being done effectively using some single variable or combination of variables, then the need for human forecasters effectively vanishes. If I or anyone else can produce such a thing, the day of human forecasters is over. There may be other reasons for the demise of human forecasters, but it seems unlikely to me that weather forecasting can be so easily distilled into an all-encompassing variable. A forecaster seeking to find such a variable is not only unlikely to be successful, but if success were achieved, s/he would be out of a job!
REFERENCES
Banacos, P.C, and D.M. Schultz, 2005: The use of moisture flux convergence in forecasting convective initiation: Historical and operational perspectives. Wea. Forecasting, 20, 351-366.
Monteverdi, J.P, C.A. Doswell III, and G.S. Lipari, 2003: Shear parameter thresholds for forecasting tornadic thunderstorms in northern and central California. Wea. Forecasting, 18, 357-370.
Sanders, F., and C.A. Doswell III, 1995: A case for detailed surface analysis. Bull. Amer. Meteor. Soc., 76, 505-521.
