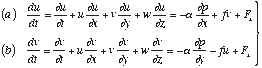 .
.
The vertical component of vorticity (which is the component most meteorologists focus on) has its own governing equation: the so-called vorticity equation.
This equation is derived by starting from the u- and v-component momentum equations:
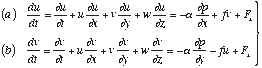 .
.
Notation here is conventional. Take the x-component partial derivative of (b) and subtract from it the y-component partial derivative of (a) - a process called cross-differentiation - which gives:
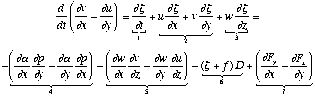 ,
,
The terms of this vorticity equation are:
Terms 1-3 are pretty obvious. Term 4 is the result of cross-differentiating the pressure gradient terms of the momentum equations, and represents the solenoidal contribution, one true "source" term. Term 5 results from cross-differentiating the vertical advection terms of the momentum equations, and represents the tilting of horizontal vorticity into the vertical. Term 6, the divergence (or "stretching") term, is the result of adding the cross-differentiation of the horizontal advection terms to the Coriolis terms in the momentum equations. Obviously, term 7 comes from cross-differentiating the friction terms in the momentum equations; it is another true "source" term.
What do I mean by a source term? If the flow starts out without any vorticity in three dimensions, then this equation shows that the only way to create vertical vorticity is through the solenoid and friction terms. Hence, they are the only true source terms. The advection terms simply redistributes existing vertical vorticity, the divergence term increases or decreases any existing vertical vorticity (including that due to Coriolis) through the action of divergence or convergence, and the tilting term changes the orientation of any existing horizontal vorticity into the vertical. There are two more such equations for the other two components of the vorticity vector, of course.
Now any treatment of the horizontal flow must involve two equations, since there are two independent momentum equations. Combining them into one equation leaves only an incomplete description of the flow. From the momentum equations, we can derive a comparable equation to the vorticity equation by cross-differentiating the other way: take the x-component partial derivative of (a) and add it to the y-component partial derivative of (b). This yields the divergence equation (where D is the horizontal divergence; see Mathematical Diversion - 1:
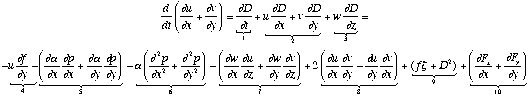
In this derivation, it is assumed that the x-coordinate is aligned east-west, and the y-coordinate is aligned north-south. The resulting equation is not very simple! Some of these terms look analogous to terms in the vorticity equation but, in general, the terms in the divergence equation are more difficult to understand. See Hess (1957; §16.4 and §16.6). Under some circumstances (notably, at synoptic-scale), most of these terms (including all of the left-hand side) can be neglected, yielding a so-called balance equation.
Finally, given the divergence and the vorticity, it can be shown that any general two-dimensional wind field can be decomposed into a nondivergent flow and an irrotational flow. This finding is known as the Helmholtz Theorem. The nondivergent flow is described by a so-called streamfunction (y) that satisfies:
and the irrotational flow is described by a so-called velocity potential (f) that satisfies:
This partitioning is only to within a vector constant. It can be shown (see Lynch 1989) that when this decomposition is done on a finite domain, the solution can include a so-called harmonic part that is both irrotational and nondivergent. It cn be described by a either a streamfunction or a velocity potential (ch) that satisfies the following:
The vector velocity, V, is given by:
where:
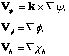
A major problem discussed in Lynch (1989) is the issue of boundary conditions when the domain is finite. I will not go into this, here.
Consider the 3- dimensional,vector equation of motion:
where: D/Dt denotes the Lagrangian time derivative (following the air); g* is the "apparent gravity" that includes the effect of centrifugal forces arising from the earth's rotation; W is the angular velocity vector of the earth; and F is the "frictional" force. Now integrate this equation around the closed boundary S of a region G on some quasi-horizontal surface:
where ds is the differential of distance around the curve S (see Fig. M4.1). The contribution from "apparent gravity" vanishes for this horizontal part of the flow, leaving only pressure gradient, Coriolis, and friction terms.
Fig. M4.1. Schematic showing the surface region G bounded by the curve S; k is a unit vector normal to the surface and ds is the increment of distance around S.
From this, it can be shown (see Bluestein 1992; pp. 253 ff.) that
Define the absolute circulation , Ca , to be
where r is a position vector on the surface that includes G, such that Dr/Dt = V. The relative circulation is C and the contribution to circulation from Coriolis is Cc . The result of all this is a circulation theorem (attributed to V. Bjerknes):
The relative circulation C is basically the integral of the tangential component of the flow around the curve S bounding G. Observe that on the basis of this theorem, there are only two ways to alter the relative circulation: a term involving density and pressure (which is related to the solenoid term in the standard meteorological vorticity equation, above) and a term involving friction. Obviously, the Coriolis contribution to the absolute circulation cannot be changed, short of changing the rotation of the Earth! By applying Stokes' Theorem:
where dA is the differential area vector element of the region G, such that dA = dA k, where k is the unit vector normal to G at any point. It can be seen that the relative circulation C is simply an area integral of the vertical component of the vorticity - put another way, relative vertical vorticity is the relative circulation per unit area (see Bluestein 1992, pp. 120 ff.):
Hess, S.L., 1957: Introduction to Theoretical Meteorology. Holt, Rhinehart, and Winston, 362 pp.
Lynch, P., 1989: Partitioning the wind in a limited domain. Mon. Wea. Rev., 117, 1492-1500.