NOTICE: This manuscript is an informal one that approaches, but doesn't attain, the status of a formal publication. It hasn't successfully negotiated the path to formal journal publication. It’s being offered here simply as the expression of my ideas regarding this topic. My readers can contact me at cdoswell & earthlink.net if they wish to discuss any of this (use the email hyperlink, or cut and paste after replacing '_&_' with '@'). If you're not willing to have your comments (and my responses) included here, don't waste my time (or yours).
NOTE: footnotes are at the end of the manuscript.
Herein, I'm exploring some ideas I've had and some of them are simply too different or too speculative for some reviewers of journal manuscripts to swallow. Since I'm not yet prepared to offer an "airtight" presentation -- one with considerable direct supporting evidence, at least -- I'm putting it out here for others to mull over. Be prepared to encounter some new perspectives ...
This manuscript was withdrawn from consideration for publication in EJSSM after I received the second round of reviews from referees. I have no wish to sully the scientific integrity of EJSSM with mere speculation ... my readers might find it interesting to compare this paper with Lemon and Doswell (1979) with respect to the level of evidence provided.
ABSTRACT
Although considerable research over the past several decades has led to extensive knowledge of environments in which supercells and tornadoes occur -- the primary examples of deep columnar convective vortices -- there has been little progress in understanding what role these rotating systems play in the atmosphere. Any comprehensive understanding of deep columnar convective vortices should include: knowledge of the energy source that powers the process, what instability mechanism is involved, and how the resulting system alters the atmosphere to mitigate the need for the process to continue. Two conceptual models have been developed that satisfy these requirements: (1) The energy source for supercells includes the storm-relative helicity of the air ascending in the updraft, in combination with the buoyancy associated with the deep convection. (2) The energy source for tornadoes is dominated by storm-relative helicity within the low-level inflow to the tornado. The instability mechanism in both is the basic exponential growth process associated with the so-called stretching term in the vertical vorticity equation -- the energy tapped from the source of helicity is used to drive the amplification of the kinetic energy of the vortex, which ultimately is dissipated by viscosity. It is suggested that the tornado model is comprehensive; it applies to all tornadoes, including mesocyclonic and nonmesocyclonic tornadoes. Although the models cannot be evaluated conclusively at this time, a plan for testing the validity of the proposed conceptual models is offered.
_____________
Supercells and tornadoes are deep columnar convective vortices (hereafter DCCVs), a modification of a similar term proposed by Snow (1987) for vortices that are "columnar" (their depth is greater than or equal to their width). The word "deep" here implies a depth on the order of the depth of troposphere. Tropical cyclone eyewalls might be another example. In the case of a supercell, this vortex is called a mesocyclone. The term mesocyclone is something of a misnomer, as it is not within the time and space scales usually associated with the term "mesoscale" (see Orlanski 1975; Emanuel 1980; Fujita 1981; Doswell 1987; Markowski and Richardson 2010, Ch. 1) -- although technically Orlanski would consider the scale of a mesocyclone "meso-γ". Markowski and Richardson view a mesocyclone as a mesoscale system, but I choose not to see it that way -- it is my understanding that the so-called "convective scale" (associated with convective clouds) is just below that of most mesoscale processes. In any case, the term "meoscyclone" has been in widespread use for decades and will be retained herein. The definition of a tornado has been problematic (as discussed at some length here) but the basic notion is that it is an intense columnar vortex, with winds near the surface capable of doing damage and is associated with a deep, moist convective cloud.
I take it as axiomatic that dynamic1 processes that can be characterized as motion systems (i.e., having kinetic energy) in the atmosphere, such as supercells and tornadoes, are not random "accidents". For most such atmospheric motion systems, some sort of known instability mechanism is involved that converts potential energy into the disturbance kinetic energy of the process in question. For example, extratropical cyclones (ETCs), are associated with baroclinic instability that taps the available potential energy (APE) associated with the thermal wind. For ordinary deep moist convection (DMC), the buoyant instability of parcel theory associated with high lapse rates in the presence of moisture converts convective available potential energy (CAPE) into the kinetic energy of the convection. Once an instability mechanism and its energy source have been identified, then the role of the process producing the weather event is usually known. Thus, ETCs redistribute heat and momentum to mitigate the meridional thermal and momentum gradients. DMC redistributes sensible and latent heat in the vertical. Analogous statements can be made for numerous other atmospheric processes.
A basic principle underlying my assertion that atmospheric motion systems have some purpose is that the atmosphere responds, when it is driven away from some state of equilibrium, so as to move back toward that equilibrium (i.e, Lechatelier's Principle). By understanding the instability and the energy source, it might be possible to propose an equilibrium state. In the preceding examples, the potential energy is the result of the atmosphere being driven by unequal heating away from equilibrium. In what follows, a very different sort of potential energy is proposed, but once that source is identified, then the purpose of the motion system is evident.
The goal of this review is to propose conceptual models that can help explain why the atmosphere "needs" supercells and tornadoes.2 What do they accomplish that is not done by some other motion system? This review offers no comprehensive new data in support of these conceptual models. Rather, arguments are presented using existing observations and already-published work to suggest that the ideas presented herein are capable of explaining certain challenging aspects of these DCCVs and their reason for existence.
Somewhat surprisingly, the very definition of a vortex is problematic (Lugt 1979). The source of difficulty with defining a vortex is the requirement that it be a closed circulation. But Galilean transformations -- those coordinate transformations involving movement of the coordinate system with a constant velocity, such as looking at the airflow in a storm-relative framework -- can alter that very property of the airflow. Clearly, a Galilean invariant way to define a vortex would be preferred, but no viable candidate has been offered, to date. In some tests (see the SPC Mesoanalysis pages under "kinematic" parameters) , I've discovered that the so-called "fluid trapping parameter" (Cohen and Schultz 2005) becomes strongly negative not just in vortices but also in regions of strong horizontal shear where negative values of the parameter are not confined a compact region. Instead, negative values can be stretched out into long filaments that no one would consider to represent a vortex, which should be roughly circular. Vorticity, although a Galilean invariant property of the airflow, is not sufficient by itself to identify a vortex because vorticity can consist entirely of shear, without any significant curvature (Viudez and Haney 1996). The "trapping parameter" is Galilean invariant, as well, but does not work as a way to identify vortices.
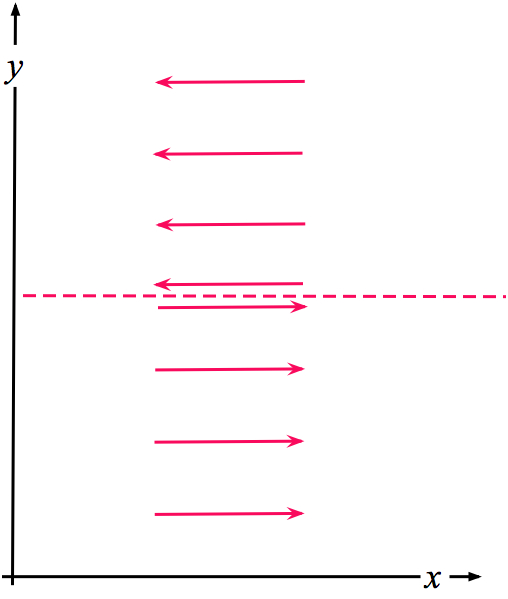
Consider the challenge associated with the abstract notion of an infinite vortex sheet (Fig. 1); the vorticity is infinite along the sheet, which extends to infinity along its length and zero elsewhere. Although the vorticity is infinite, the airflow certainly could not be considered a vortex. Therefore, no vorticity magnitude threshold can be used to define a vortex. However, an infinite vortex sheet is dynamically unstable -- a form of Kelvin-Helmholtz instability -- and tends to "roll up" into discrete vortices along its length (e.g., see Fig. 3.12 in Markowski and Richardson 2010). The action of these vortices is to redistribute the velocity difference across the sheet, transforming it to a zone of finite width with a finite vorticity gradient, rather than a line of zero width having infinite vorticity. The energy source for this instability is the transverse gradient in velocity. Kelvin-Helmholtz instability is but one example of a class of shear instabilities that derive their "potential" energy from the distribution (shear) of the wind (another example is barotropic instability).

Figure 1. A schematic showing an infinite vortex sheet in cross section (dashed red line) aligned with the x-axis of a Cartesian coordinate system. In this schematic, the y-axis can be either vertical or horizontal. The vorticity associated with this flow field is infinite along the vortex sheet and zero elsewhere.
Given that, by definition, DCCVs in the atmosphere are tied to DMC, a challenge arises when considering the role played by such vortices within the overall atmospheric system. DMC is strongly associated with positive buoyancy. DMC generally is understood as the atmosphere's way to eliminate positive buoyancy by overturning the atmosphere, responding to the excessive heat at low levels (both latent and sensible), as discussed by Doswell and Bosart (2001). This overturning process in no way requires the presence of a mesocyclone, so the issue then becomes one of explaining what supercells and tornadoes are doing that ordinary DMC is not doing.
To date, there has been no comprehensive study of the fraction of DMC storms that are supercells. It is generally accepted, albeit with incomplete evidence, that only a small percentage of DMC storms are supercells. It is problematic even to define what constitutes a DMC "storm"3, so until some evidence to the contrary emerges, it is assumed herein that supercells comprise only a few percent of all DMC events. Note that a single supercell can include a series of mesocyclones. By using certain criteria for the detection of a mesocyclone by Doppler radar (Stumpf et al. 1998), a single mesocyclone could be detected by radar several times during its life cycle. Radar-based mesocyclone detections within individual volume scans are an obvious way to document mesocyclones, but a count of mesocyclone detections is not the same as a count of supercells. As noted, there has yet to be a comprehensive climatology of supercells.
Furthermore, current evidence suggests that only around 25 percent of all mesocyclones produce tornadoes (Trapp et al. 2005), so apparently whatever purpose tornadoes are serving, the atmosphere needs relatively few of them -- supercells are uncommon, and so tornadic supercells are even less common. Absent a count of supercells, the percentage of tornadic supercells is not known, but anecdotal evidence suggests it is on the order of 25 percent.
Any comprehensive understanding of DCCVs should explain their relative rarity. The United States has more tornadoes than any other nation, but tornadoes are relatively rare even in the high frequency locations (see Brooks et al. 2003).
Tornadoes occur nearly world-wide; they have been documented on every continent except Antarctica. Although tornadoes in the tropics are relatively rare (Barnes 2001), they do occur, and not only in association with tropical cyclones. Most tornadoes are associated with supercells, but some tornadoes develop in storms that quite evidently do not have a mesocyclone prior to the tornado. They even can arise from DMC that may not have any readily detectable lightning activity. Thus, whatever role tornadoes might play in the atmosphere, they do not seem to depend on anything unique to supercells or even electrical storms.
Understanding what tornadoes are doing in the atmosphere differs from the challenge of understanding the details of tornadogenesis, although there likely is a strong relationship between them. Any comprehensive understanding of the tornado's role should also account for dominance of supercell storms in producing tornadoes, as well as the infrequency of tornadoes, by some logical means other than the rarity of convective-scale "accidents".
Section 2 reviews the extant understanding of the atmospheric role for ordinary DMC. Supercells are reviewed in section 3, which also develops a conceptual model based on that understanding. Tornadoes are considered in section 4, which includes a comparable review of existing understanding and uses that to develop a comprehensive conceptual model for tornadoes that is comparable to that for supercells. Section 5 summarizes the conceptual models and explores the kind of observations that would be needed to assess these conceptual models as directly as possible. Consideration of the impact of these models on both further research and application to severe storm forecasting is also provided.
The energy source for ordinary DMC is known -- it is commonly measured by the CAPE (Moncrieff and Miller 1976). CAPE typically is defined, using parcel theory (see Emanuel 1994, §6.3; Doswell and Markowski 2004), as the integrated thermal buoyancy through a layer from the level of free convection (LFC), to the equilibrium level (EL) at the top of the CAPE-containing layer (between the height of the LFC, zLFC and the height of the EL, zEL):
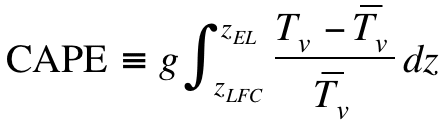 (1)
(1)
where g is the acceleration due to gravity, Tv is the virtual temperature of an adiabatically ascending air parcel as inferred from parcel theory, and ![]() is the virtual temperature within a reference environment, typically represented by a particular sounding. Parcel theory is a heavily simplified version of what is going on in the real atmosphere (as discussed in Doswell and Markowski 2004), but it suffices to describe the basic energy transformation in a convective updraft: CAPE is converted to both the kinetic energy of a DMC storm’s updraft (doing work against gravity) and the horizontal airflows associated with that updraft in order to maintain mass continuity. A comparable definition can be employed to understand the conversion of negative buoyancy (or downdraft CAPE, sometimes described as DCAPE) into the kinetic energy of convective downdrafts. As discussed in Schultz et al. (2000) and Doswell (2001), classic parcel theory results in a simplified equation for the vertical motion,
is the virtual temperature within a reference environment, typically represented by a particular sounding. Parcel theory is a heavily simplified version of what is going on in the real atmosphere (as discussed in Doswell and Markowski 2004), but it suffices to describe the basic energy transformation in a convective updraft: CAPE is converted to both the kinetic energy of a DMC storm’s updraft (doing work against gravity) and the horizontal airflows associated with that updraft in order to maintain mass continuity. A comparable definition can be employed to understand the conversion of negative buoyancy (or downdraft CAPE, sometimes described as DCAPE) into the kinetic energy of convective downdrafts. As discussed in Schultz et al. (2000) and Doswell (2001), classic parcel theory results in a simplified equation for the vertical motion,
 (2)
(2)
where ![]() is the environmental temperature (the virtual correction has been ignored -- see Doswell and Rasmussen [1994] for a discussion),
is the environmental temperature (the virtual correction has been ignored -- see Doswell and Rasmussen [1994] for a discussion), ![]() is the parcel’s lapse rate (assumed to be dry or moist adiabatic, depending on whether or not the parcel is saturated),
is the parcel’s lapse rate (assumed to be dry or moist adiabatic, depending on whether or not the parcel is saturated), ![]() is the environmental lapse rate, and z is geometric height above the surface. This equation has the simple solution,
is the environmental lapse rate, and z is geometric height above the surface. This equation has the simple solution,
![]() (3)
(3)
where zo is the parcel height at time to, i is the square root of -1, and N is the Brunt-Väisälä frequency given by
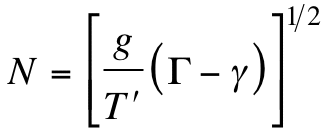 (4)
(4)
If the lapse rate exceeds the adiabatic value, N becomes imaginary and the solution (3) for parcel height grows exponentially with time. Exponential growth rate is the classical indicator of instability within the context of a mathematical model (Schultz et al. 2000).
In DMC, both updrafts and downdrafts participate in the process, in general. Warm, moist air with relatively high values of equivalent potential temperature (denoted by ![]() - see Bolton 1980; Davies-Jones 2008)4 at low levels ascends in the updraft and leaves the updraft primarily in the anvil of DMC storms. Cool and/or dry air (relatively low
- see Bolton 1980; Davies-Jones 2008)4 at low levels ascends in the updraft and leaves the updraft primarily in the anvil of DMC storms. Cool and/or dry air (relatively low ![]() ) originating above the surface descends in the downdraft, spreading out at the surface and staying there in the form of a pool of cool air. Although both an updraft and a downdraft usually are involved in the overturning process of DMC, there is no requirement that they transfer equal amounts of mass or heat. Mass continuity only requires that the mass ascending in storm updrafts be equal in mass to the descending air, but that descent need not be confined to the negatively buoyant downdraft in DMC. Compensating descent can, and often does, occur outside the convective downdraft (Hoxit et al. 1976; Stensrud and Maddox 1988; Bretherton and Smolarkiewicz 1989). The factors that create strong downdrafts are not the same as those producing strong updrafts (Wakimoto 2001). A storm with a strong updraft need not have an equally strong downdraft within the same convective storm. This possible asymmetry between the vertical heat transports in updrafts and downdrafts is a crucial issue to which I will return in the next section.
) originating above the surface descends in the downdraft, spreading out at the surface and staying there in the form of a pool of cool air. Although both an updraft and a downdraft usually are involved in the overturning process of DMC, there is no requirement that they transfer equal amounts of mass or heat. Mass continuity only requires that the mass ascending in storm updrafts be equal in mass to the descending air, but that descent need not be confined to the negatively buoyant downdraft in DMC. Compensating descent can, and often does, occur outside the convective downdraft (Hoxit et al. 1976; Stensrud and Maddox 1988; Bretherton and Smolarkiewicz 1989). The factors that create strong downdrafts are not the same as those producing strong updrafts (Wakimoto 2001). A storm with a strong updraft need not have an equally strong downdraft within the same convective storm. This possible asymmetry between the vertical heat transports in updrafts and downdrafts is a crucial issue to which I will return in the next section.
The preceding provides an abbreviated summary of the role DMC plays in the atmosphere: the energy source is associated with the presence of CAPE and DCAPE. Instability (i.e., exponential growth of small disturbances) is due to buoyancy -- both positive and negative. The end result is overturning resulting in the reduction of the energy source and, ultimately, the cessation of DMC. Note that the presence of CAPE does not mean that DMC will occur inevitably. Air parcels with CAPE generally must be lifted by some external mechanism to their LFCs before DMC can ensue. Hence, the energy for DMC can be stored in the thermal and moisture stratification and the supply can increase with time, perhaps for several days, before finally being released. And that release may not be in the same geographical location where the CAPE and DCAPE developed -- the energy can be advected considerable distances before it is released.
a. Background review
Browning is recognized as the creator of the supercell5 conceptual model, curiously enough growing out of a study of a relatively rare example in England -- the so-called Wokingham storm (Browning and Ludlam 1962). His concept was developed in greater detail by observational studies of storms in the United States (e.g., Browning 1964; Browning and Fujita 1965) and has remained a cornerstone of supercell-related research to this day (Doswell 2007). Browning’s storm model came to involve the notion that a supercell was characterized by deep, persistent rotation (Browning 1977, §4h). Doswell (1996) defined a threshold magnitude of mesocyclone vorticity arbitrarily at 10-2 s-1, having accepted Browning’s notion that the presence of a deep, persistent mesocyclone was the defining characteristic of a supercell. See Bunkers et al. (2009) for some discussion of how a mesocyclone is defined. It also was recognized early in the development of the supercell conceptual model that supercells occurred preferentially in environments with substantial vertical wind shear through a deep layer (Newton 1963). Browning and Landry (1963) and Barnes (1970) were among the first to suggest that tilting of horizontal vorticity associated with the ambient vertical wind shear could cause updrafts to rotate.
The developments of Doppler radar and numerical cloud models in the 1970s made that decade a watershed in understanding supercells. The radar presented an opportunity to observe the inner airflows of supercells, confirming many of Browning’s early ideas that had been based only on the 4-dimensional behavior of radar reflectivity. The numerical model simula-tions permitted a quantitative investigation into simulated supercell storm dynamics and the relationship between storm structure and environmental conditions. Of particular importance was the ability to explore quantitatively the relationship between the ambient vertical wind shear and the perturbation pressure field produced by the storm (Rotunno and Klemp 1982). The significance of this relationship is that the simulations demonstrated how a significant contribution to vertical motion can occur with supercells from a nonbuoyant energy source: the perturbation pressure field. The contribution from perturbation pressure (associated with thermal buoyancy) to vertical motion in ordinary DMC typically is opposed to the contribution from thermal buoyancy itself (Yau 1979), whereas supercell updrafts can be enhanced substantially by the perturbation pressure contribution: specifically, the so-called "dynamic" perturbation pressure, due to the interaction between the updraft and the ambient airflow (Rotunno and Klemp 1982).
Lemon and Doswell (1979) observed that although a supercell storm might begin as a rotating updraft, the mesocyclone at low levels evolves to lie on the gradient between updraft and downdraft. The descending air incorporated into the mesocyclone on the storm’s rear flank (Nelson 1977) is described as the storm’s "rear flank downdraft" (hereafter, RFD). The mesocyclone near the surface comes to be centered on the gradient zone between the RFD and a horseshoe- or bow-shaped updraft (Fig. 2) more or less along the RFD's gust front. Within the RFD, cloud material evaporates, forming the so-called clear slot often observed with supercells. In some supercells, the RFD is filled with descending precipitation whereas in others, the RFD is free of visible precipitation.
Davies-Jones (1984) emphasized the importance of ambient streamwise vorticity (i.e., that component of the vorticity vector that is parallel to and in the same direction as the wind vector) in a storm-relative framework for the development of a rotating updraft. A variable related to streamwise vorticity, storm-relative helicity [H(z)], is defined by
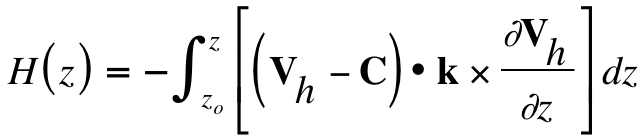
where C is the storm motion vector, and k is the unit vector in the vertical (Davies-Jones et al. 1990). Note that the quantity ![]() is that part of the horizontal vorticity vector
is that part of the horizontal vorticity vector ![]() due to the vertical shear of the horizontal wind. In the environment of a supercell, the other component of
due to the vertical shear of the horizontal wind. In the environment of a supercell, the other component of ![]() , that due to the horizontal variation of the vertical motion, generally is negligible by comparison with that due to vertical shear.6 The integrand is the storm-relative streamwise vorticity, and storm-relative helicity (hereafter, SRH) is the vertical integral of that streamwise vorticity. SRH thereby has units of m2 s-2 or, equivalently, J kg-1. These are units of energy per unit mass.
, that due to the horizontal variation of the vertical motion, generally is negligible by comparison with that due to vertical shear.6 The integrand is the storm-relative streamwise vorticity, and storm-relative helicity (hereafter, SRH) is the vertical integral of that streamwise vorticity. SRH thereby has units of m2 s-2 or, equivalently, J kg-1. These are units of energy per unit mass.
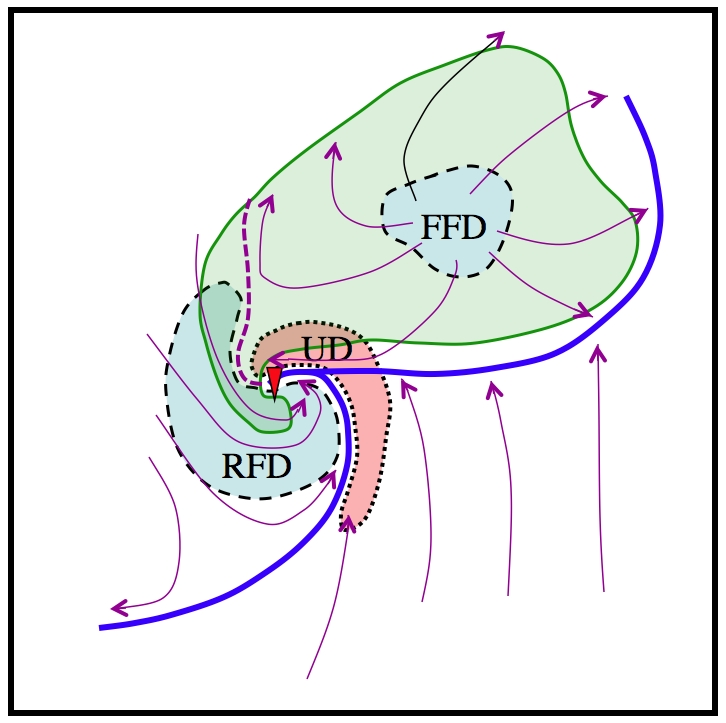
Figure 2. Schematic diagram of a supercell as seen near the surface. The light green stippling encompasses the radar echo. The gust fronts are depicted by the thick blue lines. The position of the updraft (UD) is stippled red, the forward flank downdraft (FFD) and the rear flank downdraft (RFD) are stippled blue. Streamlines of the ground-relative flow are the magenta lines with arrows indicating flow direction, and the tornado location (if present) is shown by the red triangle. Adapted from Lemon and Doswell (1979)
b. The proposed conceptual model for supercells
Although SRH seems not to constitute a form of potential energy in the conventional sense, the close relationship between ambient SRH and the occurrence of supercells seems unlikely to be a coincidence. In fact, I believe it quite plausible to suggest that the kinetic energy increase within a supercell associated with the development of a mesocyclone is drawing upon the "reservoir" of energy represented by that ambient helicity, in conjunction with the CAPE reservoir. Of course, the airflow itself represents kinetic energy, but SRH is not about the kinetic energy of the airflow, per se, but about the particular distribution of that airflow in space (in a storm-relative reference frame). It is that airflow distribution that can be thought of as a potential energy source for vortex intensification, as first suggested by Carbone (1983), albeit in the context of tornadoes rather than supercells. The idea that the distribution of airflow can be an energy source should not be so surprising, given its acceptance in the theory of shear instabilities. A supercell converts the SRH of the air flowing into its updraft from the horizontal to the vertical. Once the updraft becomes helical, stretching of that tilted streamwise vorticity within the accelerating part of the updraft amplifies the vertical vorticity to mesocyclonic proportions. Both buoyant and nonbuoyant sources of energy are present. From this perspective, supercells represent a synergistic interaction between environmental CAPE and environmental helicity.
So long as the inflow to DMC is both helical and potentially buoyant (in the sense of nonzero CAPE), then the supercell can persist. Ultimately, the formation of a DCCV is dissipative, however. Stirring a fluid with a vortex is an efficient way to promote mixing of any property. Because they are DMC storms, supercells inevitably consume CAPE, but they also must dissipate helicity. In the case of a supercell, the supply of helicity needed to maintain the mesocyclone may exceed the CAPE supply, in which case, the storm decays because the updraft's buoyancy is exhausted before it can use up its supply of energy associated with the ambient SRH. Similarly, if the CAPE supply exceeds the reservoir of SRH, the storm can evolve away from the supercellular mode, often into a squall line or bow echo. An important clue to the distinction between supercells and nonsupercellular modes is the fact that on some occasions, typically outbreaks of tornadic supercells, multiple supercells can move over very nearly the same locations. A recent example of this was the series of tornadic supercells that moved primarily from south to north along nearly identical tracks near the town of Quinter, Kansas on 23 May 2008. Apparently, the first tornadic supercell did not stabilize the environment very much, nor did the second, allowing yet a third tornadic supercell to pass over very nearly the same path. The end of the succession of supercells was associated with the formation of a squall line to the west of the supercells (Fig. 3). As that so-called "clearing line" swept through from west to east, DMC ceased in its wake. This is a relatively common sequence of events on tornado outbreak days.
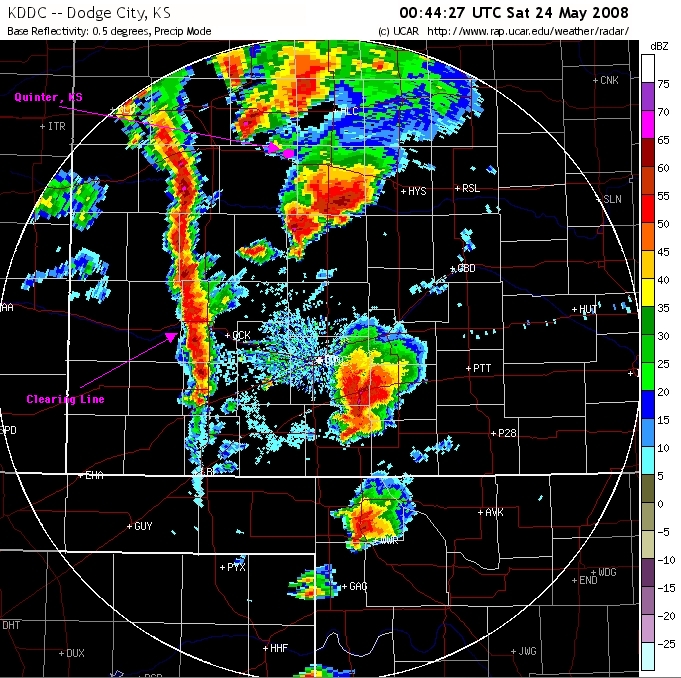
Figure 3. An example of the development of a clearing line to the west of a number of discrete supercells in the radar reflectivity display at Dodge City, KS at 0044 UTC on 24 May 2008. The approximate location of Quinter, KS is indicated with a magenta circle and the last of the tornadic supercells to affect the town has moved north of Quinter by this time. The clearing line continued to develop southward after this time and eventually moved eastward across the area within which the tornadic supercells are occurring at this time. Image from UCAR at the indicated website.
Tornadic supercells occurred in the same vicinity the day before (22 May 2008), also with multiple supercells traveling along similar paths from south to north. On 22 May, a clearing line did not develop, so an environment capable of sustaining DMC was in place the next day, whereas following the clearing line on 23 May, severe weather in the region was shut down for several days afterward.7 Squall lines apparently can be very efficient at overturning the atmosphere within a region containing CAPE and stabilizing the air in the lower troposphere, whereas supercells (especially tornadic supercells) can be rather inefficient at doing so. Otherwise, they could not be sustained when moving through areas previously traversed by predecessor tornadic supercells.
Supercells certainly consume and transform CAPE in their updrafts, but their downdrafts may not produce a large volume of air with negative buoyancy, especially when they are tornadic (Markowski et al. 2002). Supercells can consume and perhaps exhaust a pre-existing supply of high ![]() air at low levels, but at the same time fail to replace the inflow air at low levels with
air at low levels, but at the same time fail to replace the inflow air at low levels with ![]() sufficiently reduced to prevent new storms from developing. An example of this is shown in Fig. 4, where a series of supercells is observed. New supercells were developing along the outflow boundary from the first, leading supercell. The lead supercell was the primary tornado producer and the trailing supercells were mostly nontornadic. The surface winds on the inflow side of the storms were from the southeast; it is unclear the extent to which the trailing storms were experiencing surface-based inflow.
sufficiently reduced to prevent new storms from developing. An example of this is shown in Fig. 4, where a series of supercells is observed. New supercells were developing along the outflow boundary from the first, leading supercell. The lead supercell was the primary tornado producer and the trailing supercells were mostly nontornadic. The surface winds on the inflow side of the storms were from the southeast; it is unclear the extent to which the trailing storms were experiencing surface-based inflow.
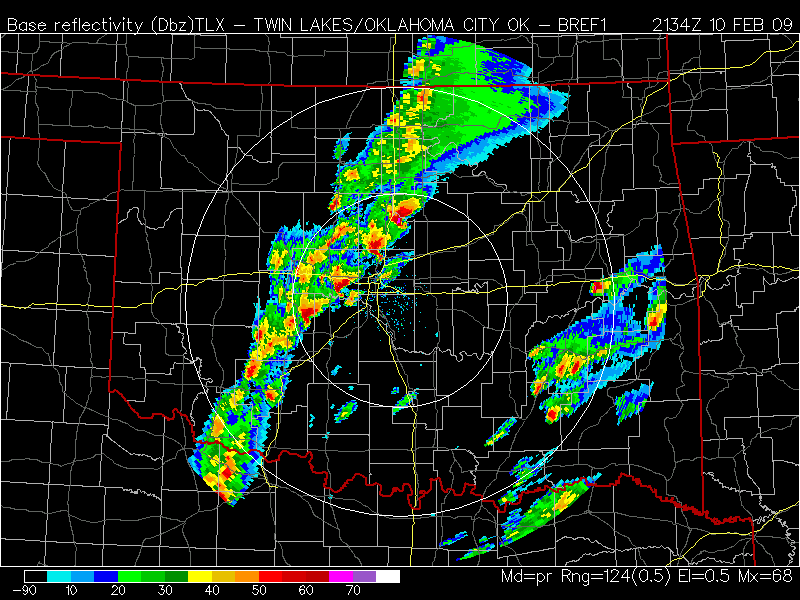
Figure 4. An example of multiple supercells following in succession on 10 Februry 2009 near Oklahoma City. Image from College of Dupage website (see here)
Those supercells that develop and maintain precipitation-filled RFDs (called high-precipitation, or HP, supercells - see Doswell and Burgess 1993) are capable of producing large volumes of low ![]() air at and near the surface. Such storms can be relatively more efficient than classic supercells (Doswell and Burgess 1993) at stabilizing a region with respect to the potential for more DMC to develop in their wake. But the persistence of mesocyclones, even when elevated above a cold pool from the storms or a pre-existing region of weak or even negative surface buoyancy (Doswell et al. 2002), suggests that such storms are also tapping a helicity source. They may be tornadic early in their evolution, but when large quantities of strongly negatively buoyant air undercut them, the tornadic phase is generally over. After that, an elevated supercell can continue for many hours.
air at and near the surface. Such storms can be relatively more efficient than classic supercells (Doswell and Burgess 1993) at stabilizing a region with respect to the potential for more DMC to develop in their wake. But the persistence of mesocyclones, even when elevated above a cold pool from the storms or a pre-existing region of weak or even negative surface buoyancy (Doswell et al. 2002), suggests that such storms are also tapping a helicity source. They may be tornadic early in their evolution, but when large quantities of strongly negatively buoyant air undercut them, the tornadic phase is generally over. After that, an elevated supercell can continue for many hours.
Supercells sometimes occur within environments that seem to be relatively poor in helicity. The cases associated with the infamous Plainfield, Illinois tornado of 28 August 1990 (see Korotky et al. 1993), or the Jarrell, Texas tornado of 27 May 1997 (Houston and Wilhelmson 2007) have posed a challenge for those proposing that a relatively deep layer of strong vertical wind shear is a necessary condition for supercells. Both of these events demonstrate that tornadic supercells occur in a wide variety of environments, from those with high SRH and low CAPE to those with comparatively low SRH and high CAPE. Sensitivity tests using numerical cloud model simulations have been carried out by varying the CAPE and vertical wind shear in controlled ways (e.g., Weisman and Klemp 1982, 1984). Generally, such simulations have not included an exhaustive or comprehensive consideration of the range of observed supercell environments, for a number of reasons. Further, CAPE-helicity diagrams for a limited number of supercell environments have been published (e.g., Johns et al. 1993; Brooks et al. 1994), seemingly suggesting that CAPE and helicity may be in some sense compensatory. That is, when the CAPE is modest, a supercell with a strong rotating updraft can still arise when the ambient helicity permits a large contribution to vertical motion through the interaction of the updraft with strong environmental shear (Markowski and Straka 2000). Or, when the CAPE is large, vertical stretching associated with strong accelerations within the updraft primarily from buoyancy can amplify modest environmental helicity, again resulting in a powerful rotating updraft.
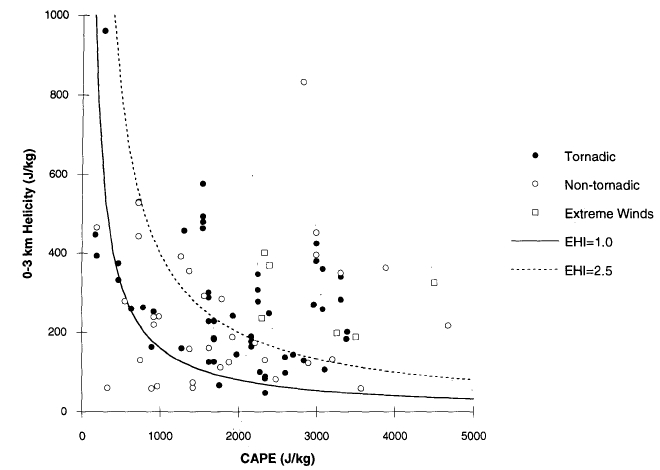
Figure 5. A CAPE-helicity diagram (using 0-3 km storm-relative helicity) showing the environments for both tornadic and nontornadic supercells. Energy-helicity index (EHI - Davies 1993) contours are also shown. From Brooks et al. (1994).
This raises the issue of storm-induced modification of its environment. Brooks et al. (1994) showed that a developing supercell storm could increase the local helicity by a factor of two or more (see their Fig. 7). Such increases are associated with storm-induced backing and strengthening of the low-level inflow to the storm as its mesocyclone strengthens. Thus, developing DMC might be able to affect its inflow helicity in a way favorable for development of a supercell. Clearly, there must be limits to this sort of "self-development", as supercells are strongly associated with environments having considerable deep-layer shear and/or helicity before any DMC is initiated. Exceptions to this can be found, however, depending on what threshold value is chosen to define the helicity value favorable for supercells to develop. Such exceptions might be tied to the challenges of observing the environmental helicity. Therefore, an important topic is the variability of helicity in time and space. Markowski et al. (1998b) have proposed that,
SRH variability may explain, in part, why some storms are tornadic and others are not in seemingly similar environments (emphasis in original text). A truly enigmatic observation that has been made by almost every astute severe storm observationalist and forecaster is why one storm produces a tornado and a nearby one does not. ... If environments with larger values of SRH are truly the ones that produce supercell tornadoes, and SRH is so variable, it might not be surprising that there is so much variability in which storms produce tornadoes.
Subsequent efforts to sample this variability have been undertaken (e.g, Markowski and Hannon 2006; Markowski and Richardson 2007), but it seems unlikely that any current or foreseeable observing systems will allow a definitive analysis of helicity’s variability. Despite its potentially large importance, the existing data simply do not permit a compelling case for a clear relationship to supercells and/or tornadoes.
A continuing point of debate exists regarding the use of storm-relative helicity versus using vertical wind shear (a Galilean invariant), which suggests that a coordinate framework moving with the storm is a "privileged" one. Helicity is not a Galilean invariant (SRH is tied to a reference frame moving with the storm, of course), so its relevance to storm dynamics has been controversial (Weisman and Rotunno 2000). This was discussed in some considerable detail by Davies-Jones (2004) who concluded:
… the mechanism for the growth of circulation around updraft perimeters also proceeds in keeping with the vertical-wind-shear viewpoint in straight shear and in accordance with the helicity perspective in circular shear. Like propagation, development of rotation in supercells depends on hodograph shape.
indicating that both perspectives are meaningful. I know of no requirement that a choice between them must be made. Rather, they are compatible and mutually interacting perspectives, each addressing different aspects of the supercell storms most directly.
The conceptual model presented herein focuses on the helicity of the storm-relative flow that enters the updraft. Storm motion is manifestly important for this conceptual model, but an accurate forecast of storm motion is not always easy to obtain from the available information (Ramsay and Doswell 2005) and involves more than the processes going on within storms. That is, storm motion can modified substantially by storm propagation, which can be influenced strongly by processes independent of the DMC storm, such as pre-existing boundaries, topography, and so forth (Zeitler and Bunkers 2005). An extensive theoretical treatment of supercell motion was done by Davies-Jones (2002), who concluded, among other things that "In all cases, tilting of storm-relative environmental streamwise vorticity explains the origins of rotation."
Some simple order of magnitude considerations can provide a basic plausibility check on this conceptual model. This is not a formal scale analysis, but is only a "plausibility" argument. A rough threshold of ambient vertical wind shear giving rise to significant helicity is of order 10-3 s-1. Over an arbitrarily-selected depth of 6 km, that represents a vector velocity difference magnitude of 6 m s-1, which is not an extremely large value. However, it is unlikely that the magnitude of the velocity difference over a 6 km deep layer would be as large as 60 m s-1, so this is at least a reasonable order of magnitude estimate for the vertical wind shear. If a mesocyclonic value of vertical vorticity is of order 10-2 s-1, this represents a tenfold increase over that initial value. If that increase is assumed to require 600 s (10 min), then it can be shown [based on Eqn (A2) in the Appendix] that the required divergence can be determined from,
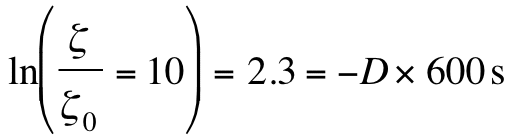 (5)
(5)
which yields a value of ![]() , a plausible value for low-level convergence at the base of a supercell updraft.
, a plausible value for low-level convergence at the base of a supercell updraft.
If an important energy source for supercells is environmental SRH, and the instability is associated with the stretching of that helical flow in the updraft, then how does the development of the mesocyclone act to mitigate the conditions giving rise to the supercell? The powerful updraft of a supercell is responsible for tilting and stretching the horizontal streamwise vorticity into the vertical vorticity of the mesocyclone. However, as parcels continue to ascend within the updraft to the storm top, they experience strong divergence once they pass the EL, and that divergence acts to "spin down" the vortex.8 It is not yet known to what magnitude the helicity is reduced above the EL in supercell storms, unfortunately. If the end result turns out to be a reduced magnitude for the helicity near the storm top compared with that at the updraft base, the net result of the supercell would be a reduction in the helicity by the supercell. In the process, the reservoir of helicity flowing through the updraft is reduced and the helicity is transformed, first by tilting (if it is horizontal), followed by stretching and amplification in the updraft through the depth where vertical motion increases with height, and finally by vertical contraction and weakening in the divergence near the storm summit.
This process is illustrated schematically in Fig. 6. The inflow to the storm is essentially horizontal and if its vorticity is streamwise (the vorticity vector is parallel to the airflow) then that inflow can be said to have SRH. As that inflow approaches the updraft, the streamwise vorticity is tilted into the vertical and amplified by the rapidly accelerating upward motion. Note that as the mesocyclone intensifies aloft, this increases the nonhydrostatic perturbation pressure gradient force contributing to vertical motion and so the updraft intensifies, in turn. This is the essential positive feedback mechanism that results in the "helicity instability". A helical flow is amplified by accelerations in the airflow parallel to the vorticity vector -- the stretching term -- and those very accelerations are amplified by nonbuoyant contributions to the vertical airflow resulting from the increasing vorticity aloft. Above the level of nondivergence, the acceleration of the vertical motion changes sign and the vorticity (and helicity) decreases rapidly with height in the strongly divergent airflow near the anvil level. The streamwise vorticity vector is tilted away from the vertical in the outflow above the level of nondivergence. If the spin down in the upper portions of the storm is such that the resulting outflow has less SRH than when it entered the supercell, the overall result is to reduce the SRH, as postulated in the conceptual model.
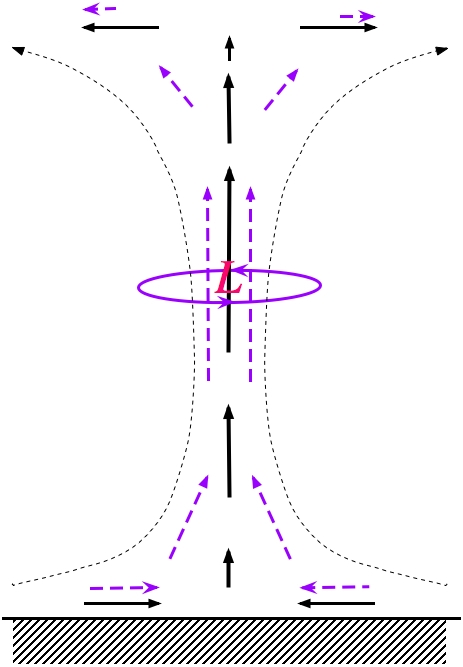
Figure 6. Supercell conceptual model, showing the vertical circulation (black solid arrows and short dashed streamlines) and the vorticity vectors (dashed purple arrows). The magnitude of the vorticity vector is indicated by its length, so the predominantly horizontal helicity of the outflow at the storm top is less than the predominantly horizontal helicity of the inflow the updraft base. The red “L” shows the mesocyclone aloft where the predominantly vertical helicity (solid purple horizontal streamline) of the airflow is large, resulting in an upward-directed perturbation pressure gradient force below this level. Compare this schematic with Fig. 7.
When an updraft is no longer being supplied with inflow that is both potentially buoyant (i.e., the inflow has no CAPE) and has streamwise vorticity, the updraft and mesocyclone will begin to dissipate. The net result of the process will be a reduction in the reservoirs of helicity and CAPE. Curiously, the RFD outflow boundary left behind by most supercells (and also by nonsupercell storms) can create low-level helicity both directly from the vertical wind shear associated with the outflow or indirectly by baroclinic generation along the boundary between the outflow and the ambient air (Klemp and Rotunno 1983; Rotunno et al. 1988; Markowski et al. 1998a).

Figure 7. A supercell storm that eventually became tornadic in South Dakota on 07 June 2005, developing on an outflow boundary marked by low clouds, extending to the left. Photograph © 2005 C. Doswell
a. Background review
Much of the modern, pioneering research about tornadoes has its roots in the needs of operational forecasters (see Doswell 2007). This includes the observation that tornadic storms tend to occur in environments characterized by strong vertical shear of the horizontal wind. That is, such storms are mostly supercells.
For tornadoes, despite their association with supercells, it’s not at all evident what the energy source for tornadoes really is. What is the instability associated with tornadoes? It has been recognized for years that tornadoes can develop rapidly - on times scales on the order of a few minutes. This seems to imply the presence of an exponentially-growing instability associated with the vorticity equation (see the Appendix).
An important question is the energy source for tornadoes. The notion has been advanced (e.g., Lilly 1982) that tornadoes ultimately derive their energy from CAPE, which leads to the idea of a so-called thermodynamic speed limit for tornadoes based on CAPE (see Fiedler and Rotunno 1986). If tornadoes are drawing their energy exclusively from CAPE, they have the same source of energy as the DMC that gives them birth. In this view, a tornado is a process within DMC that is competing with the DMC itself for the CAPE reservoir. The growth of one process would seem to inhibit the growth of the other (as implied by Lilly 1982, p. 157), who states "... the effect is to reduce the updraft, essentially transforming some of its energy into that of rotary motion." If this concept is correct, a tornado would be a parasitic process, drawing its energy from the same source as the DMC. Further, it is evidently equivalent to the concept enunciated by Lemon (1976), known as the "vortex valve" hypothesis.
An understanding of tornadoes has been elusive, in part because of their small spatiotemporal scale, and also owing to their relative rarity -- tornadoes are difficult to observe and document in detail. They are the most intense form of DCCV and are thought to represent, in the most extreme examples, the strongest windstorms of all, with windspeeds near the surface arguably as high as 150 m s-1. Tornadoes are observed most commonly with supercells, and it appears that the most intense examples are associated virtually exclusively with supercells.
Examples of tornadoes not associated with supercells include most waterspouts (although some waterspouts are produced by supercells over water) and occasional examples over land (so-called "landspouts"). Even supercells produce tornadoes that appear not to be associated directly with their mesocyclones (e.g., Fig. 8), as discussed by Wakimoto and Atkins (1996). Therefore, it is possible that a physically important distinction is between tornadoes occurring in close association with mesocyclones, versus those not associated with mesocyclones, the latter of which would include nonsupercell tornadoes.

Figure 8. An example of a storm producing both a mesocyclonic (on the right) and a nonmesocyclonic tornado (center) at the same time. The nonmesocyclonic tornado is close to the apex of the RFD gust front, and somewhat behind its leading edge. This example is on 24 May 2004, near Hebron, NE. Photograph © 2004 C. Doswell
Before the publications by Fujita (1960) and Browning 1964), the relationship of tornadoes to the deep convective storms with which they are associated was mostly unknown. That tornadoes often occurred within and near the mesocyclone of supercell storms was an important concept -- both for scientific understanding and for operational forecasters attempting to provide warning information to the public about these storms. Given that a pre-existing mesocyclone is already a reservoir of strong vertical vorticity, the connection to tornadoes seemed evident until Lemon and Doswell (1979) pointed out that mesocyclonic tornadoes do not necessarily develop in the center of the updraft region, but rather are found near the updraft-downdraft interface.
Interestingly, in a classic review paper, Ludlam (1963, p. 24) speculated that the rotation of tornadoes might have its origin on the interface between updraft and downdraft:
It is tempting to look for the spin of the tornado in the vorticity present in the general air stream as shear and tilted appropriately in the vicinity of the interface between the drafts as a consequence of the up- and down-motions.
This also was considered a central idea by Lemon and Doswell (1979), who speculated further about the role played by solenoidal generation of vorticity, as well. Ludlam (op. cit.) made another prescient comment in his review:
It may be particularly important for the intensification and persistence of a tornado that some of the downdraft air may be derived from potentially warm air … .
Ludlam somehow had anticipated the recent observations that the RFD air in tornadic supercells is unlikely to be strongly negatively buoyant (Markowski et al. 2002). The notion that tornadoes develop from the process of stretching vorticity in the vertical [i.e., Eqn (A1)] generally has been accepted for some time. Tornadic vorticity values are of order 1 s-1 (Davies-Jones 1982b). The dominance of cyclonic vorticity in tornadoes seems to suggest that there might be a direct connection to the Earth’s vorticity. Using the similar reasoning as in section 3, starting with a characteristic value for the Earth’s vorticity of 10-4 s-1in Eqn (A2), and using a divergence value of -3.8 x 10-3 s-1 (the value estimated in section 3) gives the result that
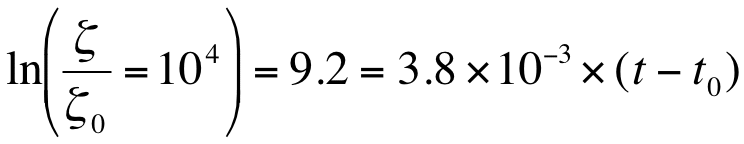
which yields a value of t-to = 2.4 x 103 s, corresponding to about 40 min. This apparently indicates that if a developing storm sustains that magnitude of convergence for 40 min, it is possible to increase ambient vorticity from that of the Earth’s "background" value to that of a tornado. This simple analysis breaks down in several ways, however. In the first place, Eqn (A1) is from a Lagrangian viewpoint, following an air parcel. For a parcel starting with the background vorticity, the time during which its initial vertical vorticity is being stretched is when the parcel is within that part of the updraft region where vertical motion increases with height. This is typically only on the order of 10 min or less -- of the right order of magnitude but arguably not enough time to create a tornado from the background value associated with the Earth’s rotation. Further, the point where the Earth’s vorticity would be stretched to tornadic magnitudes would be well above the surface, so it could not explain tornadic vorticity at the surface. If all it took was a sustained strong updraft to spin up a tornado from the background vorticity of the Earth, then tornadoes ought to be commonplace, not rare. Virtually every supercell would be tornadic.
It is now generally understood that the dominance of cyclonic rotation in tornadoes is associated with their occurrence in cyclonically-rotating supercells. Anticyclonically-rotating supercells are far from rare (Fujita and Grandoso 1968; Charba and Sasaki 1971, Klemp and Wilhelmson 1978) but they are not often tornadic (Brown and Meitín 1994; Bunkers and Stoppkotte 2007). The connection between tornadoes being predominantly cyclonic and the rotation of the Earth apparently is attributable to the importance of vertical wind shear and typical hodograph shape in supercells. Vertical wind shear through a deep layer is strongly affected by the thermal wind, which is in turn associated with the Earth’s background vorticity (i.e., the Coriolis parameter is a component of the force balance in the geostrophic wind). When combined with the typical veering wind profiles in the planetary boundary layer (Hoxit 1974; Markowski and Richardson 2010, pp. 81-82), the result is a long hodograph that curves anticyclonically with height, favoring the sustenance of cyclonic supercells (Chisolm and Rennick 1972; Weisman and Klemp 1984). Thus, the Earth’s rotation plays a role in, but is only indirectly connected to, the sense of rotation in tornadoes.
With the advent of three research capabilities in the 1970s (Doppler radar, numerical cloud models, and scientific storm chasing -- see Doswell 2007), the issue of tornadogenesis became of paramount concern, because it soon was observed that the majority of supercells are not tornadic. Even within the DCCV that is a supercell, tornadoes are rather unlikely. Brooks et al. (1994) suggested that some supercells fail to develop persistent, strong mesocyclones near the surface, which might help explain why some supercells don’t become tornadic. However, Trapp (1999) and Trapp et al. (2005b) have shown that even supercells with strong low-level mesocyclones can fail to become tornadic. Moreover, considerable evidence has accumulated that tornadoes can and do occur with storms that are not supercells (Brady and Szoke 1989; Wakimoto and Wilson 1989, Davies-Jones et al. 2001; Trapp et al. 2005b).
Maddox et al. (1980) pointed out that tornadoes often occur during the interaction between DMC storms and pre-existing boundaries (fronts, outflow boundaries, etc.), provided the storm does not move rapidly across the boundary into low-level air with strong negative buoyancy. This notion was reinforced during the so-called VORTEX (Verification of the Origins of Rotation in Tornadoes EXperiment -- Rasmussen et al. 1994) field observational campaigns of 1994-95. Markowski et al. (1998a), among others, confirmed the findings of Maddox et al. regarding the importance of pre-existing boundaries in tornadogenesis. Doswell et al. (2002) presented a case where a tornadic supercell crossed such a boundary and was persistently severe as a hailstorm for an extended period after moving into air with little or no low-level buoyancy near the surface. That boundary crossing indeed coincided with the end of the tornadic phase of that supercell, however, which also confirmed Maddox et al. (op. cit.) in that a storm crossing sufficient far across a boundary into cold, stable air at low levels has a low probability of producing a tornado.
VORTEX was an important milestone in tornado research, and subsequent field observations have demonstrated that supercells having strong negative buoyancy in their RFDs typically fail to become tornadic (Markowski et al. 2002). Field observations during and after VORTEX also have confirmed the significance of how storms interact with pre-existing baroclinic boundaries (e.g., Rasmussen et al. 2000).
Numerous studies comparing tornadic with nontornadic environments (Brooks et al. 1994; Rasmussen and Blanchard 1998; Doswell and Evans 2003; Rasmussen 2003; Thompson et al. 2003) have shown two consistent empirical results:
1. Tornadic storms tend to occur in environments with large vertical wind shear and helicity in a shallow layer near the surface (say 0-1 km).
2. Storms within environments having large dewpoint depressions (low relative humidity) tend not to be tornadic.
A complete explanation of the connection between these two empirical findings and the occurrence of tornadoes has yet to be offered. It has been suggested that large dewpoint depres-sions favor the development of cold, stable RFD outflows, which are empirically related to the non-occurrence of tornadoes. Recent work (Straka et al. 2007; Markowski et al. 2008) has indicated the importance of arched vortex lines along the RFD gust front in tornadogenesis. Tornadogenesis remains an active research topic, but the issue of the role tornadoes play in the atmosphere has not been so active.
b. The proposed conceptual model for tornadoes
A tornado is another helical DCCV, so a logical place to start in proposing the tornado’s role in the atmosphere is, again, as a means of mitigating high helicity, especially that near the surface. Some supercells produce intense vortices aloft that never quite become intense enough at the surface to be considered tornadoes, despite attaining "tornado-like" intensity down to within a hundred meters of the surface (Blanchard 2008). The very definition of a tornado as an intense vortex in contact with the surface excludes such vortices from consideration. Documentation of nontornadic but intense vortices aloft is challenging since there is no "ground truth" to confirm their presence. They can be detected only by Doppler radar at relatively close range, or by observations of nontornadic funnel clouds.9 Although the frequency with which storms produce intense vortices aloft that fail to attain tornado status (violent winds at the surface) is not known, there might be more such "near misses" than there are observed tornadoes; perhaps many more. Therefore, the relative rarity of tornadoes from supercells might be somewhat misleading. The occurrence of intense but nontornadic vortices of this small scale could still be drawing from a helicity-based energy source and might still accomplish the purpose of first intensifying and then "spinning down" that helicity, but there would be no clear surface manifestation of it, contributing to the perception that vortices of tornadic intensity are more infrequent than they really are. Nontornadic supercells that occur in environments seemingly favorable for tornadoes might be missing some as yet unknown key ingredient, but many of them might also contain tornadic intensity vortices that simply fail to reach the surface, for some reason (Trapp 1999).
The existence of intense vortices aloft within a supercell raises the issue of how likely it is that these go on to become full-fledged tornadoes. Smith and Leslie (1978) indicated that, given a vortex aloft, it might require a delicate balance of conditions for that vortex to develop downward to the surface. Leslie and Smith (1978) state that
The calculations also confirm the prediction by Morton (1969, p. 325) that the evolution of a concentrated vortex requires the forcing strength and the level of rotation to be confined within a narrow range of values; this would explain why relatively few storms spawn tornadoes. ... for a vortex to develop down to the ground, there must either be a sufficient level of ambient rotation at lower levels initially, or the vortex circulation must induce this ...
The notion that a vortex aloft could induce rotation at lower levels has been refined by Trapp and Davies-Jones (1997) within the so-called "dynamic pipe effect". The dynamic pipe effect was proposed as an explanation for how an intense vortex aloft (detectable via radar as a so-called "tornadic vortex signature", or TVS -- see Brown et al. 1978) might develop down to the surface. The downward development of vortices forming aloft was incorporated in the conceptual model of Lemon and Doswell (1979), but it has been found (Trapp et al. 1999) that many tornadoes do not develop via descent of an intense vortex (identifiable via radar as a TVS) forming initially aloft. Hence, this concept can only explain a part of the reason for the relative rarity of tornadoes from supercell storms.
The vertical mass flux within a tornado is typically only a tiny fraction of that associated with the updraft. That is, most of the air participating in the updraft of most DMC storms is not within the tornado itself (Fig. 9). Despite its high kinetic energy density, a tornado’s total kinetic energy is usually rather small compared with that of the DMC storm giving rise to it (Ludlam 1963). Hence, it seems likely that the contribution to the kinetic energy of a tornado associated with buoyant energy release from condensation within the air parcels participating in the vortex usually is modest enough to be negligible. The dynamics of an intense vortex might produce large vertical velocities but that vertical motion likely would not be driven solely by the release of CAPE from parcels within the tornadic vortex. What is needed for tornadoes is that the air parcels involved should not be strongly nega-tively buoyant, since such parcels consume energy as they are lifted, inhibiting the stretching process giving rise to the intense vortex (as noted by Leslie and Smith 1978).

Figure 9. An example illustrating the relatively small size of the tornado (just left of center, near the bottom) compared to the supercell storm updraft with which it is associated. This example is in southeastern WY on 05 June 2009. Photograph © 2009 C. Doswell
It has been suggested previously that DMC storms, and supercells in particular, can induce local changes that magnify the existing helicity beyond that present in the preconvective envi-ronment. This certainly could help explain the dominance of supercells in producing tornadoes, but it fails to answer the question of why the majority of supercells do not produce tornadoes. It may be that the resolution of this paradox may come back mostly to the issue of the static stability of the RFD outflow that is entrained into the mesocyclone. Whereas a supercell can be thought of as acting to reduce both buoyancy and helicity, the tornado per se may be dominated by the need to mitigate excessive low-level helicity. Its kinetic energy isn’t coming predominantly from converting CAPE within the parcels participating in the tornado, but rather lies in the distribution of wind velocity that results in low-level helicity. Note than an important factor in this could be tied to processes in the boundary layer near the surface [see Maddox (1993) for some discussion]. In the proposed conceptual model, it is the near-surface SRH that determines whether or not a given storm is going to be tornadic -- tilting of streamwise vorticity into the vertical by an updraft generally has been acknowledged to be incapable of explaining the presence of high vorticity at ground level (Davies-Jones 1982a,b; Davies-Jones and Brooks 1993; Wicker and Wilhelmson 1995).
The means of producing tornadic vorticity at ground level is the critical issue for producing a tornado from any storm. Recent concepts of tornadogenesis (Davies-Jones et al. 2001; Markowski et al. 2003; Straka et al. 2007; Markowski et al. 2008) have begun to focus on the RFD as a way to develop near-surface vorticity that can be stretched in an intense updraft. If helical airflow can be associated with processes occurring in a downdraft rather than an updraft, then its presence at and near the ground is relatively easy to explain. Recently, Esterheld and Guiliano (2008) have suggested that at least in some "significant" tornado (i.e., rated F2 or greater) cases, the streamwise vorticity (and SRH) in the lowest 100 m or even less might be quite large. Is the SRH from which the tornado is drawing its energy associated with the "environmental" SRH or with the processes in the RFD? Or might it include varying portions of both in specific cases? Hopefully, future observations and modeling will resolve this issue.
Note that high SRH of the airflow can be derived in two distinct ways. Some process can produce horizontal streamwise vorticity or, alternatively, substantial vertical vorticity can be present at the foot of an updraft (and thereby be predominantly streamise). Recent concepts involving arched vortex lines (Straka et al. 2007; Markowski et al. 2008) indicate the former can happen during the descent of the RFD, resulting in near-vertical vortex lines near the base of the updraft, which in turn could result in tornadogenesis when those vortex lines are stretched in an updraft.
On the other hand, the generally accepted process for producing tornadoes from nonsupercell storms begins with pre-existing vertical vorticity maxima near the ground that subsequently can be stretched when overrun by a strong updraft. In the case of a pre-existing region of vertical vorticity, the airflow is not necessarily characterized by SRH in the environment until that vorticity maximum is overrun by the updraft. The action of the tornado in either case, however, is to consume that SRH by means of a DMC storm’s updraft, first amplifying the streamwise vorticity and then weakening it aloft as that updraft region becomes strongly divergent.
According to this simple concept, CAPE likely would be a poor discriminator between tornadic and nontornadic storms. Observations have shown repeatedly (e.g., Johns et al. 1993; Monteverdi et al. 2003, Shafer et al. 2009) that this is the case. Tornadic storms occur in a wide range of CAPE values, even near zero (e.g., Carbone 1983). Supercells, in particular, are effective at producing intense updrafts because they can draw upon nonbuoyant energy sources for vertical motion. Earlier, it was noted that helicity, especially through shallow layers near the surface, has been found to be an important discriminator for tornadoes, which is consistent with this conceptual model. It also has mentioned that high low-level relative humidity (low temperature-dewpoint spread) is an important factor for avoiding the production of strong negative buoyancy in downdrafts, so its value in discriminating tornadic from nontornadic supercells can be understood.
Many nontornadic supercells could be producing tornado-like vortices aloft that fail to reach the surface. These intense vortices would have the same role as tornadoes -- consuming environmental helicity -- but simply fail to reach the surface, perhaps because the helicity near the surface is not sufficient to initiate the instability. The rarity of tornadoes would not mean that tornado-like vortices are anywhere near so rare, but most of them do not affect the surface.
Some recent notions presented by Lewellen and Lewellen (2007a,b) concern the possible importance of the so-called "corner flow collapse" mechanism in producing intense vortices at the surface. However, at this time, it is not evident that such a mechanism offers any insight regarding the relative rarity of tornadoes.
In summary, the proposed conceptual models are based on the notion that the presence of storm-relative environmental helicity represents an energy source for exponential growth of vertical vorticity in the updraft of a DMC storm. In the case of a supercell, the helicity and buoyancy provided by CAPE combine to amplify both the vertical vorticity and the updraft’s vertical velocity. That is, the updraft is driven both by CAPE and by nonbuoyant processes associated with perturbation pressure gradients arising because of vertical wind shear in the environment. Nonbuoyant augmentation of the updraft allows supercells to become severe even in low CAPE environments. Near the storm top, strong divergence acts to spin down the mesocyclone rapidly and to disperse excess heat at low levels into upper troposphere-lower stratosphere levels. A supercell storm ceases if it consumes, or is cut off from, its supply of inflow with CAPE. If the supply of helicity in the inflow is exhausted, the storm may continue so long as a CAPE reservoir can be tapped, but it will lose its supercell characteristics. A nonsupercell storm can become supercellular if it encounters enhanced environmental helicity (see Burgess and Curran 1985). In any case, some or all of the pre-existing helicity will have been used to develop the mesocyclonic vorticity and is exported to upper levels in the storm, where it is dissipated. When a supercell ends, any residual kinetic energy of the mesocyclone ultimately is consumed by viscosity.
It has been proposed herein that a tornado taps the energy of the low-level SRH, in particular, and the air parcels within the tornadic circulation contribute only trivial buoyant energy for amplifying the vorticity through release of latent heat in the vortex airflow. Thus, the tornado is not necessarily a parasitic process that diminishes CAPE that would otherwise power the updraft.10 Instead, the tornado uses the existing storm updraft (which may or may not be using mostly CAPE to develop strong ascent) to amplify the streamwise vorticity associated with helicity near the surface. If there is some theoretical energy-based limit to the speed of winds in a tornado, it likely is not the thermodynamic parameter, CAPE. An important thermodynamic constraint, however, is that the air flowing into the vortex should not be strongly stable to ascent, which would inhibit the stretching process necessary for the instability. All that is needed to produce an intense vortex is helical inflow combined with intense stretching along the streamwise direction. DMC storms provide the intense stretching, but the storm environment provides the helicity in the inflow to the DMC storm (or the potential helicity, in the case of nonsupercell storms). Many intense vortices (which, for the most part, are undocumented) could be present in nontornadic storms, simply because they fail to become intense enough at the surface to meet the criteria for a tornado. Such tornado-like vortices may be considerably more common that the existing record of tornadoes might suggest. There is no systematic record kept of nontornadic vortices in DMC.
An important issue unanswered herein by these conceptual models is how the horizontal scale of a DCCV is determined. As proposed, a supercell involves an interaction between the effects of buoyancy and of helicity to produce a mesocyclone (which always includes a rotating updraft). The scale selection process that determines the horizontal scale of DMC storms may be what dominates the horizontal scale of a supercell (roughly equal to its vertical scale), as well.
A tornado's horizontal scale is at least one order of magnitude less than that in the vertical. Perhaps this is a result of the dominance of low-level processes in a tornado -- the amplification of the vortex may be predominantly in the lowest several hundred meters, resulting in a horizontal vortex of relatively small diameter. There is also a horizontal scale reduction inherent in the contraction associated with the vertical stretching process.
Existing publications provide evidence that is consistent with these conceptual models, but that evidence is far from compelling in support of what is presented here. Ideally, data collected specifically to test these hypotheses would be more convincing than I can be in this review. What sort of data would be needed to establish the validity of these conceptual models?
For the supercell, collecting sounding data ahead of and in the wake of supercell and nonsupercell storms would be needed. The idea would be to determine as accurately as possible the detailed time and space distribution of storm-relative helicity in the storm inflow, and then in the wake of the storm. Studies involving soundings from operational fixed sounding sites generally have an unsatisfactory relationship to the individual storms because such sites are rarely in the proper position and their soundings are unlikely ever to be taken at the appropriate times to measure the environment both immediately before and immediately after storm passage. The sparse distribution of operational soundings in time and space precludes much new insight regarding these storm-scale issues.
Some means of obtaining numerous soundings ahead of, and in the wake of both supercell and nonsupercell storms would be needed. Dropwindsondes released from high-flying air-craft (Hock and Franklin 1999) on the margins of DMC storms might be satisfactory. Such a study is complicated by the fact that DMC storm outflows can be characterized by considerable low-level helicity, whether the storms that produced them are supercells or not. A storm might consume pre-existing helicity but also can create new horizontal (or vertical) helicity in its wake. Thus, even a field experiment with frequent soundings surrounding a DMC storm might not provide completely unambiguous evidence for this conceptual model. However, there still could be considerable insight gained by observing in detail how supercells modify their environment, especially in comparison with how nonsupercell storms modify theirs.
If data could be obtained on a tornado outbreak day with multiple tornadic supercells passing over similar paths, it would be revealing to document, with soundings in front of and behind the supercells, how much modification of the buoyancy (and helicity) is associated with successive tornadic supercell passage. If, as postulated in section 2, there appears to be an absence of strongly stable stratification near the surface behind such a storm, this could confirm (or refute) the concept that such storms are inefficient at reducing the buoyancy of the low-level air that supports the development of new supercells in the wakes of their predecessors.
Another aspect of the conceptual model for supercells is the rapid "spin-down" of the mesocyclonic vorticity near the storm top. It would be important to see whether or not the helicity of the outflow near the storm top was indeed smaller than that of the inflow at the storm base. It might be possible to use airborne Doppler radar from high-flying aircraft to provide detailed information about the airflow at upper levels in the storm, perhaps in combination with ground-based mobile Doppler radars. If the resulting helicity in that upper-level outflow region is less than that of the inflow, despite having its vorticity increased to mesocyclonic values by stretching in the lower parts of the storm, this would indicate that a supercell is indeed ultimately dissipating the energy implicit in the helicity of the inflow, averaged over the depth of the storm.
The conceptual supercell model could be tested by sampling in detail the variability of helicity in the vicinity of DMC storms, including both supercells and nonsupercells, and consider-ing the helicity in the post-storm environment, as well. As already noted, helicity is a volatile variable and its spatial and temporal variation near DMC storms has yet to be sampled to a satisfactory degree (Markowski et al. 1998b). To what extent are regions of large helicity of sufficient area and persistent enough to qualify as "reservoirs" that can be tapped (and consumed) by DMC storms? Does a supercell ultimately reduce the helicity overall?
The use of numerical cloud models could be a powerful tool for assessing the plausibility of these conceptual models. The key to using them is to diagnose the simulations so as to reveal the time and space distribution of helicity. If the basic ideas embodied in Fig. 6 can be verified in a numerical simulation, this would add considerably to their plausibility. Of course, it is understood that numerical models have their limitations but they should contain enough essential dynamics to determine how helicity is distributed in space and how it changes with time in a supercell.
A persistent issue that has arisen many times but never resolved in a satisfactory way is the extent to which DMC storms can modify their immediate environment so as to increase the likelihood of their becoming supercells. Numerical model simulations (Brooks et al. 1994) indicate that in the immediate vicinity of a mesocyclone, the local wind field can have substantially increased helicity, despite starting from horizontally homogeneous initial conditions. This increased helicity must be associated with the horizontal streamwise vorticity of the inflow. It is not known what limits the capacity of DMC storms to "bootstrap" themselves into supercell mode, but given the relative rarity of supercell storms, especially in environments characterized by weak vertical wind shear, it would seem that there must be such limits.
Some part of the evidence being collected in field projects, including VORTEX2, aimed at understanding tornadogenesis may prove to be useful to assess the conceptual model proposed herein for tornadoes. One observing effort that would be helpful would be to determine the frequency of tornado-like vortices aloft in supercells that fail to go on to become fully-developed tornadoes. Knowing how frequently such elevated but intense vortices occur in supercell storms would be relevant to the conceptual models herein. The difference between a tornadic supercell and a nontornadic supercell has become somewhat blurred -- Rasmussen and Blanchard (1998) have suggested that many supercells that produce weak tornadoes occur in environments that more closely resemble nontornadic storms than those supercells that include one or more "significant" (rated F2/EF2 or higher) tornadoes. Thompson et al. (2003) found similar results.
Another effort that would be of value in assessing these proposed conceptual models is to learn more about the behavior of the airflow near the top of a tornado (or a tornadic intensity vortex aloft), which may or may not also be very near the storm top itself. Is there large enough divergence at the top of such a vortex that it would act to reduce the SRH at the storm top below that of the air flowing into the vortex at low levels? Again, high-altitude aircraft with Doppler radar capability would be helpful with regard to such questions.
The intention of this review has been to develop conceptual models that can be used to explain why the atmosphere "needs" supercells and tornadoes. Given that a reasonably complete physical understanding for atmospheric processes always includes an explanation of what and why those processes are doing what they do, it seems very much worthwhile to direct some effort to gain this understanding. It is inconceivable to me that DCCVs serve no purpose; that they are simply atmospheric "accidents" resulting from the juxtaposition of a storm with the right environment. Although I am unable to provide herein a completely satisfactory demonstration of the validity of these conceptual models, at the very least I would hope to stimulate more discussion of this topic and to encourage the collection of field data that might permit deeper insight than what I have provided herein.
Acknowledgments I thank Prof. Jeff Trapp (Purdue University) for his encouragement to my pursuit of this topic. Dr. Russ Schneider (NOAA/Storm Prediction Center) engaged me in some stimulating discussions that eventually led to the development of the hypotheses presented herein. Prof. Trapp, Dr. Harold Brooks (NOAA/National Severe Storms Laboratory), Dr. Chad Shafer (Univ. of South Alabama), Roger Edwards (NOAA/Storm Prediction Center), and Les Lemon (NOAA/Weather Decision Training Branch) offered valuable critical comments on early versions of this manuscript. My EJSSM reviewers (Prof. Paul Markowski, Dr. Dan Dawson, Dr. Matt Bunkers, and Prof. Matt Parker) are acknowledged for many useful comments and suggestions that have improved this manuscript, but I absolve them of having to accept any responsibility for any content of this paper with which they might take issue. Any mistakes or outright errors are my own, naturally.
Consider the following highly-simplified vertical vorticity equation that considers only the effect of divergence on the vorticity:
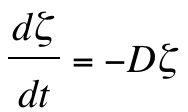 (A1)
(A1)
where D is the kinematic divergence and ![]() is the vertical component of the vector vorticity
is the vertical component of the vector vorticity ![]() , and where V is the three-dimensional vector wind, which has Cartesian components
, and where V is the three-dimensional vector wind, which has Cartesian components ![]() in pressure coordinates in which
in pressure coordinates in which ![]() is the vertical motion. Vh is the horizontal wind vector and
is the vertical motion. Vh is the horizontal wind vector and ![]() is the horizontal vorticity vector. This greatly simplified equation reflects the basic notion that the divergence term is the one that typically creates the largest time rate of change of vertical vorticity in supercells (see Brandes 1984). Note that the vertical vorticity component is a relative vorticity that can have either sign. When D can be assumed to be a constant, the solution to Eqn (A1) is given by
is the horizontal vorticity vector. This greatly simplified equation reflects the basic notion that the divergence term is the one that typically creates the largest time rate of change of vertical vorticity in supercells (see Brandes 1984). Note that the vertical vorticity component is a relative vorticity that can have either sign. When D can be assumed to be a constant, the solution to Eqn (A1) is given by
![]() (A2)
(A2)
where ![]() . In the presence of divergence, the mass continuity equation in isobaric coordinates,
. In the presence of divergence, the mass continuity equation in isobaric coordinates,
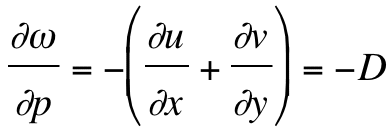 (A3)
(A3)
requires there must be changes in vertical motion with height (pressure). According to (A2) any preexisting positive vertical vorticity can grow exponentially when D is negative (i.e., the flow is convergent, implying an increase in the magnitude of upward vertical motion with height). Exponential growth, as with Eqn. (3) in the text, is the classic indication of an instability. This instability is present only when the flow is helical -- when airflow is parallel to the vorticity vector and the vorticity is being "stretched" by that airflow. That this concept is closely associated with the rapid intensification of tornadoes is well known.
Barnes, G., 2001: Severe local storms in the tropics. Severe Convective Storms, Meteor. Monogr., 28, no. 50, Amer. Meteor. Soc., 359–432.
Barnes, S. L., 1970: Some aspects of a severe, right-moving thunderstorm deduced from mesonet rawinsonde observations. J. Atmos. Sci., 27, 634–648.
Blanchard, D.O., 2008: Interactions between a supercell and a quasistationary frontal boundary. Mon. Wea. Rev., 136, 5199–5210.
Bolton, D., 1980: The computation of equivalent potential temperature. Mon. Wea. Rev., 108, 1046–1053.
Brady, R. H., and E. J. Szoke, 1989: A case study of monmesocyclone tornado development in northeast Colorado: Similarities to waterspout formation. Mon. Wea. Rev., 117, 843–856.
Brandes, E. A., 1984: Vertical vorticity generation and mesocyclone sustenance in tornadic thunderstorms: The observational evidence. Mon. Wea. Rev., 112, 2253–2269.
Bretherton, C. S., and P. K. Smolarkiewicz, 1981: Gravity waves, compensating subsidence and detrainment around cumulus clouds. J. Atmos. Sci., 46, 740–759.
Brooks, H. E., C. A. Doswell III, and J. Cooper, 1994: On the environments of tornadic and nontornadic mesocyclones. Wea. Forecasting, 9, 606–618.
______, ______, and M. P. Kay, 2003: Climatological estimates of local daily tornado probability in the United States. Wea. Forecasting, 18, 626–640.
Brown, R. A., and R. J. Meitín, 1994: Evolution and morphology of two splitting thunderstorms with dominant left-moving members. Mon. Wea. Rev., 122, 2052–2067
______, L. R. Lemon, and D. W. Burgess, 1978: Tornado detection by pulsed Doppler radar. Mon. Wea. Rev., 106, 29–38.
Browning, K. A., 1962: Cellular structure of convective storms. Meteor. Mag., 91, 341–350.
______, 1964: Airflow and precipitation trajectories within severe local storms which travel to the right of the winds. J. Atmos. Sci., 4, 634–639.
______, 1977: The structure and mechanism of hailstorms. A Review of Hail Science and Hail Suppression, Meteor. Monogr., 16, No. 38, Amer. Meteor. Soc., 1–39.
______, and F. H. Ludlam, 1962: Airflow in convective storms. Quart. J. Roy. Meteor. Soc., 88, 117–135.
______, and C. R. Landry, 1963: Airflow within a tornadic thunderstorm. Preprints, 10th Weather Radar Conf., Washington, D.C., Amer. Meteor. Soc., 116–122.
______, and T. Fujita, Eds., 1965: A Family Outbreak of Severe Local Storms -- A Comprehensive Study of the Storms in Oklahoma on 26 May 1963, Part 1. AFCRL Special Rep. No. 32, AFCRL-45-695(1), 346 pp. [NTIS Accession No. AD-623787].
Bunkers, M. J., and J. W. Stoppkotte, 2007: Documentation of a rare tornadic left-moving supercell. Electronic J. Severe Storms Meteor., 2(2), 1–22.
______, D. R. Clabo, and J. W. Zeitler, 2009: Comments on 'Structure and formation mechanism on the 24 May 200 supercell-like storm developing in a moist environment over the Kanto Plain, Japan.' Mon. Wea. Rev., 137, 2703–2712.
Burgess, D. W., and E. B. Curran, 1985: The relationship of storm type to environment in Oklahoma on 25 April 1984. Preprints, 14th Conf. on Severe Local Storms, Indianapolis, IN, Amer. Meteor. Soc., 208–211.
Carbone, R. E., 1983: A severe frontal rainband. Part II: Tornado parent vortex circulation. J. Atmos. Sci., 40, 2639–2654.
Charba, J. P., and Y. Sasaki, 1971: Structure and movement of the severe thunderstorms of 3 April 1964 as revealed from radar and surface mesonetwork data analysis. J. Meteor. Soc. Japan, 49, 191–214.
Chisholm, A. J. , and J. H. Renick, 1972: The kinematics of multi-cell and su- percell Alberta hailstorms. Research Council of Alberta Hail Studies Rep. 72-2, 24–31.
Cohen, R. A., and D. M. Schultz, 2005: Contraction rate and its relationship to frontogenesis, the Lyapunov exponent, fluid trapping, and airstream boundaries. Mon. Wea. Rev., 133, 1353–1369
Davies, J. M., 1993: Hourly helicity, instability, and EHI in forecasting supercell tornadoes. Preprints, 6th Conf. Severe Local Storms, Chicago, IL, Amer. Meteor. Soc., 218–221.
Davies-Jones, R., 1982a: A new look at the vorticity equation with application to tornadogenesis. Preprints, 12th Conf. on Severe Local Storms, Orlando, FL, Amer. Meteor. Soc., 269–272.
______, 1982b: Observational and theoretical aspects of tornadogenesis. Intense atmospheric vortices, L. Bengtsson and J. Lighthill, Eds., Springer-Verlag, 175–189.
______, 1984: Streamwise vorticity: The origin of updraft rotation. J. Atmos. Sci., 41, 2991–3006.
______, 2002: Linear and nonlinear propagation of supercell storms. J. Atmos. Sci., 59, 3178–3204.
______, 2004: Growth of circulation around supercell updrafts. J. Atmos. Sci., 61, 2863–2876.
______, 2008: An efficient and accurate method for computing the wet-bulb temperature along pseudoadiabats. Mon. Wea. Rev., 136, 2764–2785.
______, and H. E. Brooks, 1993: Mesocyclogenesis from a theoretical perspective. The Tornado: Its Structure, Dynamics, Prediction and Hazards (Geophys. Monogr. 79), C. Church, Ed., Amer. Geophys. Union, 105–114.
______, D. Burgess, and M. Foster, 1990: Test of helicity as a tornado forecast parameter. Preprints, 16th Conf. Severe Local Storms, Kananaskis Park, AB, Canada, Amer. Meteor. Soc., 588–592.
______, R. J. Trapp, and H. B. Bluestein, 2001: Tornadoes and tornadic storms. Severe Convective Storms, Meteor. Monogr., 28, No. 50, Amer. Meteor. Soc., 167–221.
Doswell, C. A. III, 1987: The distinction between large-scale and mesoscale contribution to severe convection: A case study example. Wea. Forecasting, 2, 4–16.
______, 1996: What is a supercell? Preprints, 18th Conf. Severe Local Storms (San Francisco, CA), Amer. Meteor. Soc., 641.
______, 2001: Severe convective storms -- An overview. Severe Convective Storms, Meteor. Monogr., 28, no. 50, Amer. Meteor. Soc., 1–26.
______, 2007: Historical overview of severe convective storms research. Electronic J. Severe Storms Meteor., 2(1), 1–25.
______, and D. W. Burgess, 1993: Tornadoes and tornadic storms: A review of conceptual models. The Tornado: Its Structure, Dynamics, Hazards, and Prediction (Geophys. Monogr. 79), Amer. Geophys. Union, 161–172.
______, and E. N. Rasmussen, 1994: The effect of neglecting the virtual temperature correction on CAPE calculations. Wea. Forecasting, 9, 625–629.
______, and L. F Bosart, 2001: Extratropical synoptic-scale processes and severe convection. Severe Convective Storms, Meteor. Monogr., 28, No. 50, Amer. Meteor. Soc., 27–69.
______, and J. S. Evans, 2003: Proximity sounding analysis for derechos and super-cells: An assessment of similarities and differences. Atmos. Res., 67-68, 117–133.
______, and P. M. Markowski, 2004: Is buoyancy a relative quantity? Mon. Wea. Rev., 132, 853–863.
______, D.V. Baker and C.A. Liles. 2002: Recognition of negative mesoscale factors for severe weather potential: A case study. Wea. Forecasting, 17, 937–954.
Emanuel, K. A., 1980: Forced and free mesoscale motions in the atmosphere. Collection of Lecture Notes on Dynamics of Mesometeorological Disturbances, Y. K. Sasaki, N. Monji, and S. Bloom, Eds., Cooperative Institute for Mesoscale Meteorological Studies, 120 David L. Boren Blvd, Suite 2100, Norman, OK 73072, 189–259.
______, 1994: Atmospheric Convection. Oxford University press, 580 pp.
Esterheld, J. M. and D. J. Giuliano, 2008: Discriminating between tornadic and nontornadic supercells: A new hodograph technique. Electronic J. Severe Storms Meteor., 3 (2), 1–50.
Fiedler, B. H., and R. Rotunno, 1986: A theory for the maximum windspeeds in tornado-like vortices. J. Atmos. Sci., 43, 2328–2340.
Fujita, T., 1960: A Detailed Analysis of the Fargo Tornadoes of June 20, 1957. Research Paper No. 42, U.S. Weather Bureau, Washington, D.C., 1-67. [out of print]
______, 1981: Tornadoes and downbursts in the context of generalized planetary scales. J. Atmos. Sci., 38, 1511–1534.
______, and H. Grandoso, 1968: Split of a thunderstorm into anticyclonic and cyclonic storms and their motion as determined from numerical model experiments. J. Atmos. Sci., 25, 416–439.
Hock, T. F., and J. L. Franklin, 1999: The NCAR GPS dropwindsonde. Bull. Amer. Meteor. Soc., 80, 407–420.
Houston, A. L., and R. B. Wilhelmson, 2007: Observational analysis of the 27 May 1997 central Texas tornadic event. Part I: Prestorm environment and storm maintenance /propagation. Mon. Wea. Rev., 135, 701–726.
Hoxit, L. R., 1974: Planetary boundary layer winds in baroclinic conditions. J. Atmos. Sci., 31, 1003–1020.
______, C. F. Chappell, and J. M. Fritsch, 1976: Formation of mesolows or pressure troughs in advance of cumulonimbus clouds. Mon. Wea. Rev., 104, 1419–1428.
Johns, R. H., J. M. Davies, and P. W. Leftwich, 1993: Some wind and instability parameters associated with strong and violent tornadoes. 2. Variations in the combinations of wind and instability parameters. The Tornado: Its Structure, Dynamics, Hazards, and Prediction (Geophys. Monogr. 79), Amer. Geophys. Union, 583–590.
Klemp, J. B., and R. B. Wilhelmson, 1978: The simulation of three-dimensional convective storm dynamics. J. Atmos. Sci., 35, 1070–1096.
______, and R. Rotunno, 1983: A study of the tornadic region within a supercell thunderstorm. J. Atmos. Sci., 40, 359–377.
Korotky, W., R. W. Przybylinski, and J. A. Hart, 1993: The Plainfield, Illinois, tornado of August 28, 1990: The evolution of synoptic and mesoscale environments. The Tornado: Its Structure, Dynamics, Hazards, and Prediction (Geophys. Monogr. 79), Amer. Geophys. Union, 611–624.
Lemon, L. R., 1976: Tornadic storm evolution: Vortex valve hypothesis. Appendix G, The Union City, Oklahoma Tornado of 24 My 1973, R. A. Brown, Ed., NOAA Tech Memo ERL NSSL-80, 229–234.
______, and C. A. Doswell III, 1979: Severe thunderstorm evolution and mesocyclone structure as related to tornadogenesis. Mon. Wea. Rev., 107, 1184–1197.
Leslie, L. M., and R. K. Smith, 1978: The effect of vertical stability on tornadogenesis. J. Atmos. Sci., 35, 1281–1288.
Lewellen, D. C., and W. S. Lewellen, 2007a: Near-surface intensification of tornado vortices. J. Atmos. Sci., 64, 2176–2194.
______, and ______, 2007b: Near-surface vortex intensification through corner flow collapse. J. Atmos. Sci., 64, 2195–2209.
Lilly, D. K., 1982: The development and maintenance of rotation in convective storms. Intense Atmospheric Vortices (L. Bengtsson and J. Lighthill, Eds.), Springer-Verlag, 149–160.
Ludlam, F. H., 1963: Severe local storms. A review. Severe Local Storms, Meteor. Monogr., 5, No. 27, Amer. Meteor. Soc., 1–30.
Lugt, H. J., 1979: The dilemma of defining a vortex. Recent Developments in Theoretical and Experimental Fluid Mechanics: Compressible and Incompressible Flows. (A79-29651 11-34) Springer-Verlag, 309–321.
Maddox, R. A., 1993: The diurnal low-level wind oscillation and storm-relative helicity. The Tornado: Its Structure, Dynamics, Hazards, and Prediction (Geophys. Monogr. 79), Amer. Geophys. Union, 591–598.
______, L. R. Hoxit, and C. F. Chappell, 1980: A study of tornadic thunderstorm interactions with thermal boundaries. Mon. Wea. Rev., 108, 322–336.
Markowski, P. M., and J. M. Straka, 2000: Some observations of rotating updrafts in a low-buoyancy, highly sheared environment. Mon. Wea. Rev., 128, 449–461.
______, and C. Hannon, 2006: Multiple-Doppler radar observations of the evolution of vorticity extrema in a convective boundary layer. Mon. Wea. Rev., 134, 355–374.
______, and Y. Richardson, 2007: Observations of vertical wind shear heterogeneity in convective boundary layers. Mon. Wea. Rev., 135, 843–861.
______, and ______, 2010: Mesoscale Meteorology in Midlatitudes. Wiley-Blackwell, 407 pp.
______, E. N. Rasmussen, and J. M. Straka, 1998a: The occurrence of tornadoes in supercells interacting with boundaries during VORTEX-95. Wea. Forecasting, 13, 852–859.
______, J. M. Straka, E. N. Rasmussen, and D. O. Blanchard, 1998b: Variability of storm-relative helicity during VORTEX. Mon. Wea. Rev., 126, 2959–2971.
______, J. M. Straka, and E. N. Rasmussen, 2002: Direct surface thermodynamic observations within rear-flank downdrafts of nontornadic and tornadic supercells. Mon. Wea. Rev., 130, 1692–1721.
______, J. M Straka, and E. N. Rasmussen, 2003: Tornadogenesis resulting from transport of circulation by a downdraft: Idealized numerical simulations. J. Atmos. Sci., 60, 795–823.
______, Y. Richardson, E. Rasmussen, J. Straka, R. Davies-Jones, and R. J. Trapp, 2008: Vortex lines within low-level mesocyclones obtained from pseudo-dual-Doppler radar ob-servations. Mon. Wea. Rev., 136, 3513–3535.
Moncrieff,. M. W., and M. .J. Miller, 1976: The dynamics and simulation of tropical cumulonimbus and squall lines. Quart. J. Roy. Meteor. Soc., 120, 373–94.
Monteverdi, J. P., C. A. Doswell III, and G. S. Lipari, 2003: Shear parameter thresholds for forecasting tornadic thunderstorms in north-ern and central California. Wea. Forecasting, 18, 357–370.
Morton, B. R., 1969: The strength of vortex and swirling core flows. J. Fluid Mech., 38, 315–333.
Nelson, S. P., 1977: Rear flank downdraft: A hailstorm intensification mechanism. Preprints, 10th Conf on Severe Local Storms, Omaha, NE, Amer. Meteor. Soc., 521–525.
Newton, C. W., 1963: Dynamics of severe convective storms. Severe Local Storms, Meteor. Monogr., 5, No. 27, Amer. Meteor. Soc., 33–58.
Orlanski, I., 1975: A rational subdivision of scale for atmospheric processes. Bull. Amer. Meteor. Soc., 56, 527–530.
Ramsay, H. A., and C. A. Doswell III, 2005: A sensitivity study of hodograph-based methods for estimating storm motion. Wea. Forecasting, 20, 954–970.
Rasmussen, E. N., 2003: Refined supercell and tornado forecast parameters. Wea. Forecasting, 18, 530–535.
______, and D. O. Blanchard, 1998: A baseline climatology of sounding-derived supercell and tornado forecast parameters. Wea. Forecasting, 13, 1148–1164.
______, J. M. Straka, R. Davies-Jones, C. A. Doswell III, F. H. Carr, M. D. Eilts, and D. R. MacGorman, 1994: Verification of the origins of rotation in tornadoes experiment: VORTEX. Bull. Amer. Meteor. Soc., 75, 995–1006.
______, S. Richardson, J. M. Straka, P. M. Markowski, and D. O. Blanchard, 2000: The association of significant tornadoes with a baroclinic boundary on 2 June 1995. Mon. Wea. Rev., 128, 174–191.
Rotunno, R., and J. B. Klemp, 1982: The influence of the shear-induced pressure gradient on thunderstorm motion. Mon. Wea. Rev., 110, 136–151.
______, ______, and M. L. Weisman, 1988: A theory for strong, long lived squall-lines. J. Atmos. Sci., 45, 463–485.
Schultz, D. M., P. N. Schumacher, and C. A. Doswell III, 2000: The intricacies of instabilities. Mon. Wea. Rev., 128, 4143–4148.
Shafer, C. M., A. E. Mercer, C. A. Doswell III, M. B. Richman, and L. M. Leslie, 2009: Evaluation of WRF forecasts of tornadic and nontornadic outbreaks when initialized with synoptic-scale input. Mon. Wea. Rev., 137, 1250–1271.
Smith, R. K., and L. M. Leslie, 1978: Tornadogenesis. Quart. J. Roy. Meteor. Soc., 104, 189–199.
Snow, J. T., 1987: Atmospheric columnar vortices. Rev. Geophys., 25 (3), 371–385.
Stensrud, D. J., and R. A. Maddox, 1988: Opposing mesoscale circulations: A case study. Wea. Forecasting, 3, 189–204.
Straka, J. M, E. N. Rasmussen, R. P. Davies-Jones, and P. M. Markowski, 2007: An observational and idealized numerical examination of low-level counter-rotating vortices in the rear flank of supercells. Electronic J. Severe Storms Meteor., 2(8), 1–22.
Stumpf, G. J., A. Witt, E. D. Mitchell, P. L. Spencer, J. T. Johnson, M. D. Eilts, K. W. Thomas, and D. W. Burgess, 1998: The National Severe Storms Laboratory mesocy-clone detection algorithm for the WSR-88D. Wea. Forecasting, 13, 304–326.
Thompson, R. L., R. Edwards, J. A. Hart, K. L. Elmore, and P. Markowski, 2003: Close proximity soundings with supercell environments obtained from the Rapid Update Cycle. Wea. Forecasting, 18, 1243–1261.
Trapp, R. J., 1999: Observations of nontornadic low-level mesocyclones and attendant tornadogenesis failure during VORTEX. Mon. Wea. Rev., 127, 1693–1705.
______, and R. Davies-Jones, 1997: Tornadogenesis with and without the dynamic pipe effect. J. Atmos. Sci., 54, 113–133.
______, E. D. Mitchell, G. A. Tipton, D. W. Effertz, A. I. Watson, D. L. Andra, Jr., and M. A. Magsig, 1999: Descending and non-descending tornadic vortex signatures detected by WSR-88Ds. Wea. Forecasting, 14, 625–639.
______, G. J. Stumpf, and K. L. Manross, 2005a: A reassessment of tornadic mesocyclones. Wea. Forecasting, 20, 680–687.
______, S. A. Tessendorf, E. S. Godfrey, and H. E. Brooks, 2005b: Tornadoes from squall lines and bow echoes. Part I: Climatological distribution. Wea. Forecasting, 20, 23–34.
Viudez, A., and R. L. Haney, 1996: On the shear and curvature vorticity equations. J. Atmos. Sci., 53, 3384–3394.
Wakimoto, R. M., 2001: Convectively driven high wind events. Severe Convective Storms, Meteor. Monogr., 28, no. 50, Amer. Meteor. Soc., 255–298.
______, and J. W. Wilson, 1989: Nonsupercell tornadoes. Mon. Wea. Rev., 117, 1113–1140.
______, and N. T. Atkins, 1996: Observations on the origins of rotation: The Newcastle tornado during VORTEX 94. Mon. Wea. Rev., 124, 384–407.
Weisman, M. L., and J. B. Klemp, 1982: The dependence of numerically simulated convective storms on vertical wind shear and buoyancy. Mon. Wea. Rev., 110, 504–520.
______, and ______, 1984: The structure and classification of numerically simulated convective storms in directionally varying wind-shears. Mon. Wea. Rev., 112, 2479–2498.
______, and R. Rotunno, 2000: The use of vertical wind shear versus helicity in interpreting supercell dynamics. J. Atmos. Sci., 57, 1452–1472.
Wicker, L. J., and R. B. Wilhelmson, 1995: Simulation and analysis of tornado development and decay within a three-dimensional supercell thunderstorm. J. Atmos. Sci., 52, 2675–2703.
Yau, M. K., 1979: Perturbation pressure and cumulus convection. J. Atmos. Sci., 36, 690–694.
Zeitler, J. W., and M. J. Bunkers, 2005: Operational forecasting of supercell motion: Review and case studies using multiple datasets. Nat. Wea. Dig., 29, 81-97.
_____________
1 As opposed to kinematic processes (e.g., frontogenesis) that have no scale associated with them and cannot be distinguished in terms of dynamic mechanisms.
2 Note that this does not imply that I believe the atmosphere has a conscious need for a purpose in the way that humans do. This wording is metaphorical, not literal.
3 For example, how many DMC "storms" should be counted for a squall line? Does every cell constitute a separate storm or is a connected line of cells just one storm?
4 Note that a moist pseudoadiabat has a constant value of ![]() , so this variable is a useful tool for diagnosing buoyant instability (discussed in some detail by Schultz et al. 2000)
, so this variable is a useful tool for diagnosing buoyant instability (discussed in some detail by Schultz et al. 2000)
5 The term “supercell” was used first in the formal literature by Browning (1962).
6 On the scale of a supercell, however, the contribution to horizontal vorticity from the horizontal gradient of vertical motion could be important, notably on the interface between the updraft and the RFD.
7 This sequence of events was associated with an ETC -- the passage of its trough aloft through the area on 23 May was apparently connected with development of the clearing squall line.
8 This is similar to another DCCV, the eyewall of a strong tropical cyclone.
9 Some believe that a funnel cloud is by definition a nontornadic vortex aloft. Although many tornadoes do produce funnel clouds, not all tornadoes have condensation funnels, not all funnel clouds associated with tornadoes actually reach the surface, and many funnel clouds are nontornadic.
10 If this is the case, then the notion of a thermodynamic speed limit for tornado winds is not generally valid. In some rare instances, an extremely large tornado (e.g., diameter > 2 km) might have meaningful contribution to its potential energy from CAPE (as in the large tornadoes produced on 4 May 2007 in and near Greensburg, KS).